|
|
|
|
|
|
|
|
Gegeben ist ein gleichseitiges Dreieck 
.
Berechnen Sie das Verhältnis der Flächeninhalte von Inkreis und Umkreis
dieses Dreiecks.
Lösung:
Die Abbildung
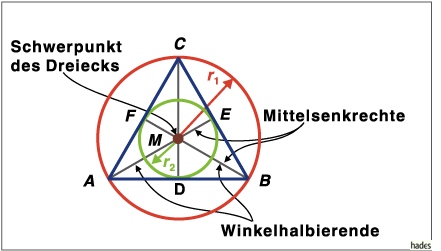
zeigt ein gleichseitiges Dreieck. Der Mittelpunkt des Inkreises wird durch den Schnittpunkt der Winkelhalbierenden bestimmt. Der Mittelpunkt des Umkreises wird durch den Schnittpunkt der Mittelsenkrechten festgelegt. In einem gleichseitigen Dreieck sind Winkelhalbierende und Mittelsenkrechte identisch.
In einem gleichseitigen Dreieck gilt 
und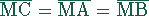 
.
Außerdem folgt aus den Ähnlichkeitssätzen
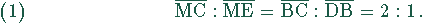
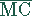ist der Radius 
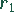des Umkreises und
ist der Radius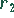 
des Inkreises.
Für die Flächeninhalte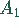 
des Umkreises und 
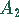des Inkreises gilt
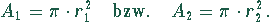
Aus (1) folgt
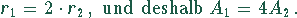
Die Flächeninhalte von Inkreis und Umkreis bei einem gleichseitigen
Dreieck verhalten sich wie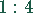 
.
