Viereck/Sechszehneck

In einem Quadrat der Seitenlänge a werden die Mittelpunkte der Seiten mit den Eckpunkten verbunden. Diese Strecken schneiden sich. Es ensteht ein nichtkonvexes Sechzehneck (siehe Abildung).

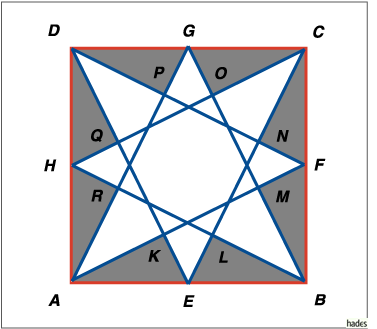
Wie groß ist der Flächeninhalt in dem Sechzehneck?

Lösung:

Den gesuchten Flächeninhalt erhält man, indem von dem Flächeninhalt des Quadrates ABCD die Summe der Flächeninhalte der acht blau umrandeten Dreiecke

subtrahiert werden.

Folgende Dreiecke sind kongruent

Sie stimmen jeweils in zwei Seiten und den von ihnen eingeschlossenem rechten Winkel überein.

Deshalb sind die grünen Dreiecke ebenfalls kongruent, denn sie stimmen in allen Winkeln und einer Seite überein. An einem Beispiel soll dies demonstriert werden. Wir betrachten ohne Beschränkung der Allgemeinheit die Dreiecke .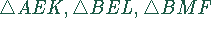

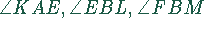1. Die Winkel sind gleich, da sie zu den kongruenten Dreiecken 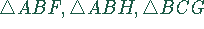gehören.
2. Das gleiche gilt für die Winkel .
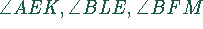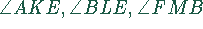3. Die Winkel sind gleich, da die jeweiligen zwei anderen Winkel gleich sind.

Es gilt ferner 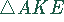ist dem Dreieck 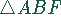ähnlich, da sie in zwei Winkeln übereinstimmen. Deshalb muß der Winkel rechtwinklig sein.

Aus den Strahlensätzen folgt

d.h.,wegen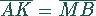

Mit Hilfe des Pythagoras kann die Strecke berechnet werden:

Daraus folgt

Der Flächeninhalt des rechtwinkligen Dreiecks 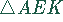beträgt

Wegen der Kongruenz aller Dreiecke ergibt sich für den Flächeninhalt des Sechzehnecks