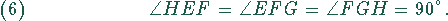|
|
|
|
|
|
|
|
Zeichnen Sie ein Parallelogramm. Errichten Sie auf jeder Seite nach außen ein Quadrat. Die Mittelpunkte dieser Quadrate bilden ein Viereck.
Beweisen Sie, daß dieses Viereck ein Quadrat ist.
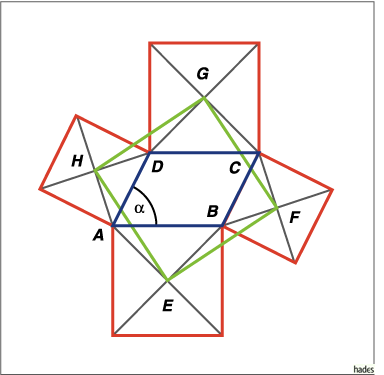
Lösung:
Den Winkel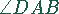 
bezeichnen wir mit 
. Dabei nehmen wir ohne
Beschränkung der Allgemeinheit an, daß 
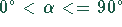ist.
Dann gilt
und
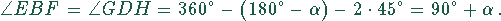
Also sind alle Winkel
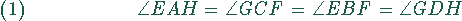
gleich.
Ferner gilt als halbe Diagonale in kongruenten Quadraten
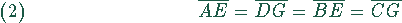
bzw.
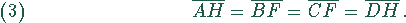
Aus (1),(2),(3) folgt
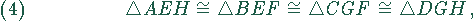
also
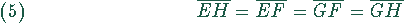
und 
.
Der Winkel 
ist
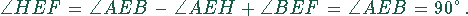
Eine ähnliche Überlegung gilt für die Winkel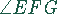 
und 
.
Wegen (5) und (6) ist EFGH ein Quadrat.
