|
|
|
|
|
|
|
|
Gegeben ist ein Rechteck mit den Seitenlängen a und b. Über jeder Seite wird außerhalb des Rechteckes ein Halbkreis gezeichnet. Außerdem wird der Umkreis des Rechtecks konstruiert.
Man berechne die Summe der Flächeninhalte der in der Abbildung
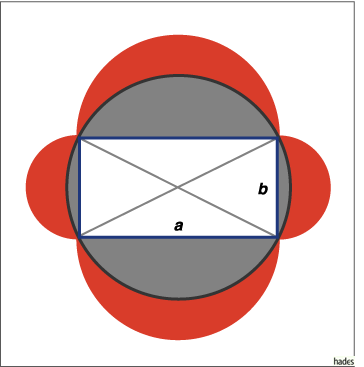
rot gezeichneten sichelförmigen Flächen.
Lösung:
Die Halbkreise über den Rändern des Rechtecks haben folgende Flächen
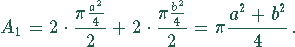
Der Umkreis um das Rechteck hat seinen Mittelpunkt im Schnittpunkt der Diagonalen d
und damit einen Radius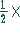 
Diagonalenlänge:
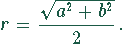
Das ergibt eine Fläche für den Umkreis von
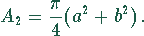
Die grauen Kreissegmente haben die Fläche
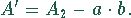
Die roten sichelförmigen Flächen ergeben sich aus
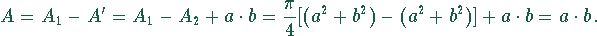
Die Summe der roten sichelförmigen Flächeninhalte ist gleich dem
Flächeninhalt des Rechtecks.
