|
|
|
|
|
|
|
|
Gegeben sei ein Kreis mit dem Durchmesser d. In diesem Kreis werden zwei
Kreise mit den Durchmessern 
und 
so eingezeichnet,
daß sich die Kreise in einem Punkt berühren. Dabei gilt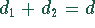 
und
.
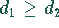Der Flächeninhalt der in der Abbildung rot umrandeten Fläche soll ein Maximum haben.
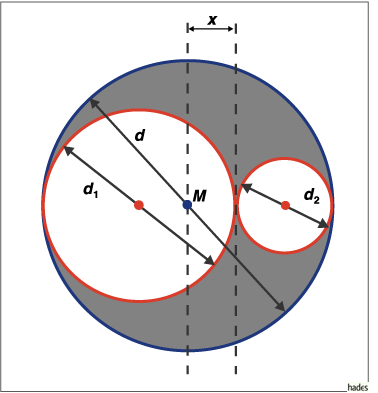
Wie groß muß 
sein?
Lösung:
Der Flächeninhalt des großen Kreises ist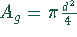 
.
Die Flächeninhalte der kleinen Kreise sind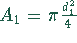 
und
.
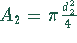Der Flächeninhalt der rot umrandeten Fläche ist dann
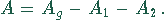
Der Abstand des Mittelpunktes M des großen Kreises von dem Berührungspunkt der kleineren Kreise sei x. Dann gilt
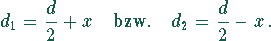
Damit ergibt sich für die Fläche A
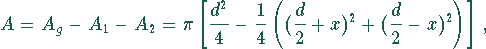
bzw.
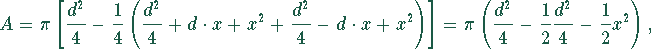
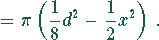
Der Flächeninhalt der rot umrandeten Fläche wird maximal, wenn
ist. D.h., die beiden kleineren Kreise sind gleich groß und haben den
halben Durchmesser des großen Kreises.
