|
|
|
|
|
|
|
|
Bestimmen Sie die Grenzwerte folgender Funktionen
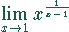
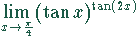
Lösung:
Zur Lösung der Aufgabe benutzt man die Regel von de l'Hospital.
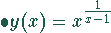
In diesem Fall ist es zweckmäßig, die Funktion zu logarithmieren und dann den Grenzwert zu bilden.
Da sowohl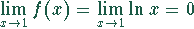 
als auch
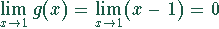ist, kann die
Regel von de l'Hospital angewendet werden.
Damit ergibt sich der Grenzwert
Da dies der Logarithmus des Grenzwertes ist, ergibt sich für den Grenzwert
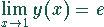
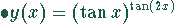
Auch in diesem Fall ist es zweckmäßig, die Funktion zunächst zu logarithmieren und dann den Grenzwert zu bilden.
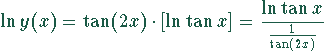
Führt man nun den Grenzübergang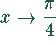 
durch,
so findet man, daß sowohl Zähler als auch Nenner gegen Null streben. Deshalb
kann die Regel von de l'Hospital auf diese Aufgabe angewendet werden.
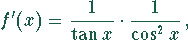
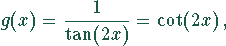
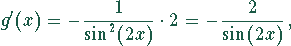
Beim Grenzübergang ergibt sich
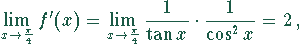
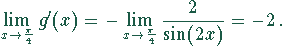
Der Grenzwert der logarithmierten Funktion errechnet sich damit zu
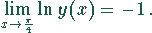
Der Grenzwert der Funktion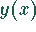 
beim Grenzübergang 
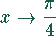nimmt den Wert 
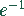an.
