Gerade und ungerade Funktionen

Zerlegen Sie die folgenden Funktionen in eine Summe von Funktionen 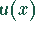und 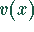, wobei 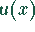eine gerade und 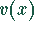eine ungerade Funktion ist. Stellen Sie sowohl 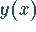als auch 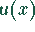und 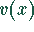graphisch dar.

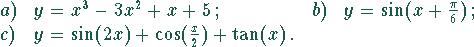
Lösung:

a)

Für die graphische Darstellung benutzen Sie Mathematica oder MapleV.

Mathematica

Plot[{x^3-3 x^2+x+5,x^3+x,5-3 x^2},{x,-10,10},
PlotStyle->{{RGBColor[0,0,0]},{RGBColor[1,0,0]},
{RBGColor[0,0,1]}}]

MapleV

plot({x^3-3*x^2+x+5,x^3+x,5-3*x^2},{x=-10..10,-110..10);

b) Die Sinusfunktion muß mit Hilfe der Additionstheoreme für trigonometrische Funktionen zerlegt werden:

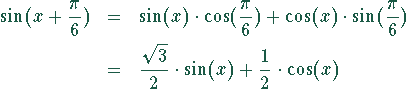
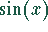ist eine ungerade Funktion und 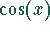eine gerade Funktion. D.h.

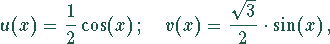
Mathematica

Plot[{Sin[x+Pi/6],(1/2) Sqrt[3] Sin[x],(1/2) Cos[x]},
{x,-10,10},PlotStyle->{{RGBColor[0,0,0]},
{RGBColor[1,0,0]},{RGBColor[0,0,1]}}]

MapleV

plot({sin(x+Pi/6),(1/2)*sqrt(3)*sin(x),(1/2)*cos(x)},
x=-10..10,-10..10);

c) Die Tangensfunktion ist wie die Sinusfunktion eine ungerade Funktion. Deshalb gilt:

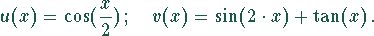
Mathematica

Plot[{Sin[2 x]+Cos[x/2]+Tan[x],Sin[2 x], Cos[x/2]+Tan[x]},
{x,-10,10},PlotStyle->{{RGBColor[0,0,0]},
{RGBColor[1,0,0]},{RGBColor[0,0,1]}}]

MapleV

plot({sin(2*x)+cos(x/2)+tan(x),sin(2*x),cos(x/2)+tan(x)},
x=-10..10,-10..10);