|
|
|
|
|
|
|
|
Bestimmen Sie die Eigenschaften der Funktionen
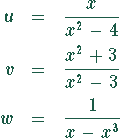
Lösung:
Es ist zweckmäßig, sich die Funktionen mittels Mathematica oder MapleV graphisch darzustellen.
:
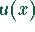Mathematica
Plot[x/(x^2-4),{x,-10,10}]
MapleV
plot(x/(x^2-4),x=-10..10);
Definitonsbereich: 
Wertebereich: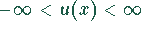 
Quadrant: Für 
liegt die Funktion 
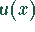im ersten und vierten Quadranten.
Für 
liegt die Funktion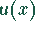 
im zweiten und dritten Quadranten.
Periodizität: nein
Monotonie: Im ganzen Definitionsbereich monoton fallend
Symmetrie: ungerade Funktion, Punktsymmetrie zum Ursprung
Asymptoten:
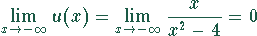
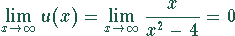
Spezielle Werte
Nullstellen: 
Sprungstellen: keine
Polstellen: 
Extremwerte: keine
Wendepunkte: keine
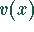
Mathematica
Plot[(x^2+3)/(x^2-3),{x,-10,10}]
MapleV
> plot((x^2+3)/(x^2-3),x=-10..10);
Definitonsbereich: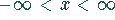 
Wertebereich: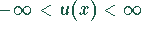 
Quadrant: Für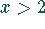 
liegt die Funktion 
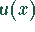im ersten Quandranten.
Für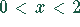 
liegt die Funktion 
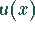im vierten Quadranten.
Für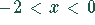 
liegt die Funktion 
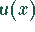im dritten Quadranten.
Für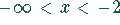 
liegt die Funktion 
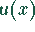im zweiten Quadranten.
Periodizität: nein
Monotonie: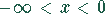 
monoton wachsend
Für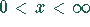 
monoton fallend
Symmetrie: gerade Funktion, Spiegelsymmetrie zur y-Achse
Asymptoten:
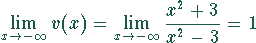
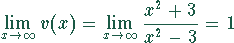
Spezielle Werte
Nullstellen: keine
Sprungstellen: keine
Polstellen: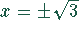 
Extremwerte: 
relatives Maximum
Wendepunkte: keine
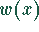
Mathematica
Plot[1/(x-x^3),{x,-10,10}]
MapleV
> plot(1/(x-x^3),x=0.1..2); > plot(1/(x-x^3),x=-2..0.1);
Definitonsbereich: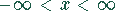 
Wertebereich: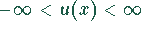 
Quadrant: Für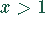 
liegt die Funktion 
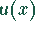im vierten Quandranten.
Für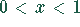 
liegt die Funktion 
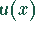im ersten Quadranten.
Für 
liegt die Funktion 
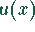im dritten Quadranten.
Für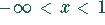 
liegt die Funktion 
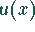im zweiten Quadranten.
Periodizität: nein
Monotonie: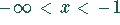 
monoton wachsend
Für 
monoton wachsend
Für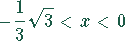 
monoton fallend
Für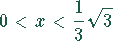 
monoton wachsend
Für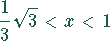 
monoton fallend
Für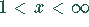 
monoton fallend
Symmetrie: ungerade Funktion
Asymptoten:
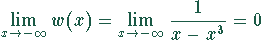
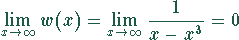
Spezielle Werte
Nullstellen: keine
Sprungstellen: keine
Polstellen: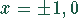 
Extremwerte: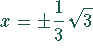 
relative Extremwerte
Wendepunkte: keine
