Kubische Funktion

Diskutieren Sie die Funktion

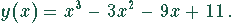
Lösung:

Die Nullstellen liefert die Gleichung

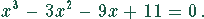
Diese kubische Gleichung kann man mit dem HORNER-Schema lösen.

Mittels Mathematikprogramme, z.B. Mathematica und MapleV, kann diese kubische Gleichung ebenfalls gelöst werden.

Lösung mittels des HORNER-Schemas.

Eine Nullstelle findet man durch Probieren bei . Damit kann man einen Linearfaktor abspalten

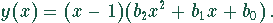
Die Zerlegung ergibt

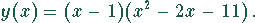
Die Nullstellen des zweiten Faktor können durch Lösen der quadratische Gleichung

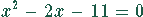
erhalten werden:

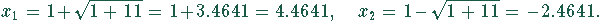
Damit erhalten wir für die Lösungsmenge der Nullstellen .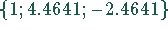

Der Definitionsbereich ist 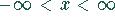. Zur Bestimmung der Extremwerte und der Wendepunkte müssen die erste und zweite Ableitung gebildet werden:

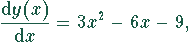
Durch Nullsetzen der ersten Ableitung und Lösen der quadratischen Gleichung erhält man die Lage der Extremwerte

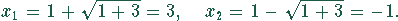
Die Extremwerte von y liegen bei 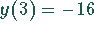und .

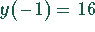Der Wendepunkt ergibt sich, wenn man die zweite Ableitung Null setzt und diese Gleichung löst:

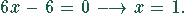
Der zugehörige y-Wert ergibt sich aus der Ausgangsgleichung, wenn eingesetzt wird: .

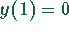Die Grenzwerte der Funktion sind

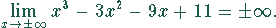
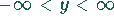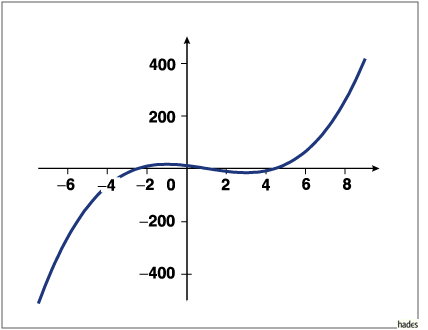
Der Wertebereich liegt zwischen . Damit kann die Kurve leicht skizziert werden.

Mathematica

y:=x^3-3x^2-9x+11
1.Ableitung
y1=D[y,x]
2.Ableitung
y2=D[y1,x]
Nullstellen
Solve[y==0,x]
Extremwerte
Solve[y1==0,x]
f[x_]:=x^3-3 x^2-9 x+11
f[x]
f[-1]
f[3]
Wendepunkt
Solve[y2==0,x]
f[1]
Plot[y,{x,-5,5}]

MapleV

> y:=x^3-3*x^2-9*x+11.;
> y1:=diff(y,x);
> y2:=diff(y1,x);
> solve(y=0,x);
> solve(y1=0,x);
> subs(x=3,y);
> subs(x=-1,y);
> solve(y2=0,x);
> subs(x=1,y);
>plot(y,x=-5..5);