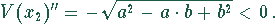Kubische Funktion/Materialminimierung

Aus einem rechteckigem Blech soll ein Trog mit maximalem Volumen gebaut werden. Wie groß müssen die quadratischen Ecken sein, die ausgeschnitten werden müssen, um einen Trog mit maximalem Volumen abzukanten?

Lösung:

Die Blechtafel hat die Abmessungen(Skizze)

• Länge a
• Breite b
• Breite und Länge des ausgeschnittenen Quadrats x

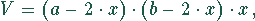
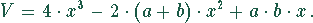
Das Volumen ist ein Polynom 3. Grades. Die Extremwerte findet man durch Nullsetzen der ersten Ableitung.

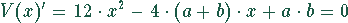
Das ist eine quadratische Gleichung. Zur Lösung bringt man die quadratische Gleichung auf ihre Normalform. Dann wird und . Damit ergeben sich als Lösungen:

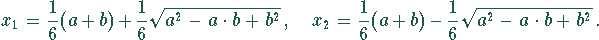
Damit das Volumen ein Maximum annimmt, muß die zweite Ableitung an der Stelle kleiner Null sein.

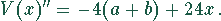
Setzt man in diese Gleichung ein, so ergibt sich

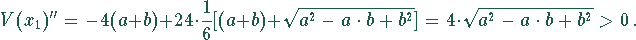
An dieser Stelle ist die zweite Ableitung größer Null, und deshalb besitzt das Volumen für den Wert ein Minimum.

Für ergibt sich für die zweite Ableitung

Für nimmt das Volumen ein Maximum an.