Hyperbolische Funktionen

Lösen Sie die Gleichungen:

a)

b)

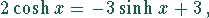
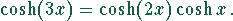
Lösung:

a)

Aus den Umrechnungsformeln für Hyperbelfunktionen folgt

Eine Umformung der Ausgangsgleichung ergibt

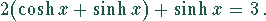
Mit der Umrechnungsformel folgt daraus

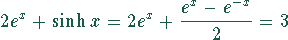
bzw.

Diese Gleichung läßt sich einfach durch Multiplikation beider Seiten mit umformen:

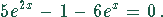
An dieser Stelle ist es zweckmäßig, die Substitution einzuführen. Damit ergibt sich eine quadratische Gleichung

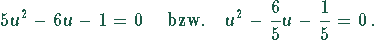
Die Lösung der quadratischen Gleichung ergibt

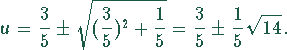
Den gesuchten Wert für x erhält man durch Logarithmieren der Größe u. Da der Logarithmus nur für positive Werte definiert ist, existiert nur eine Lösung

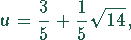
die logarithmiert werden kann. Man erhält als Lösung

b)

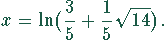
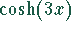In den Umrechnungsformeln findet man Beziehungen für und 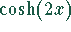. Werden diese Beziehungen in die Ausgangsgleichung eingesetzt, ergibt sich die Gleichung

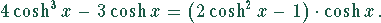
Durch Ausmultiplizieren der rechten Seite und Umformung erhält man

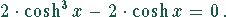
Daraus kann man kürzen:

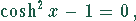
bzw.