Newton-Verfahren/Flüssigkeitsspiegel in einem zylindrischen Tank

Ein liegender zylindrischer Kessel mit gegebenem Grundkreisradius R hat ein Fassungsvermögen von 1500 Liter. Er ist mit 900 Liter Flüssigkeit

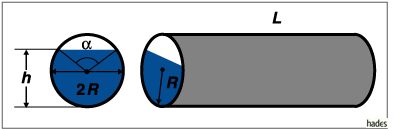
gefüllt. Wie hoch steht der Flüssigkeitsspiegel?

Anmerkung: Die sich im Rechengang ergebende nichtlineare Gleichung ist mittels des Newton-Verfahrens zu lösen.

Lösung:

Die gesuchte Höhe kann nach der Beziehung

berechnet werden. Dazu wird aber der Zentriwinkel benötigt. Diesen erhält man aus dem Verhältnis Füllmenge/Gesamtvolumen. Das Gesamtvolumen des Zylinders ist

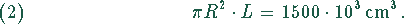
Daraus errechnet sich die Länge des Zylinders zu

Die Füllmenge kann aus zwei Anteilen errechnet werden:

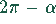• dem Volumen, das sich aus dem roten Kreisausschnitt mit dem Winkel als Grundfläche und der Höhe L ergibt, und
• dem Volumen, das aus dem hellblauen Dreieck als Grundfläche und der Höhe L besteht.

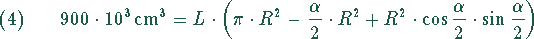
Dies läßt sich mit Hilfe der Additionstheoreme für trigonometrsiche Funktionen umformen:

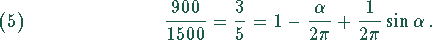
Daraus ergibt sich die nichtlineare Gleichung für

Diese Gleichung läßt sich nach dem Newton-Verfahren lösen.

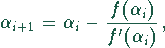
wobei

ist.

Als nullte Näherung schätzen wir , dann ergibt sich

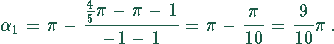
In zweiter Näherung erhält man

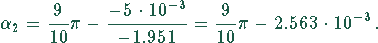
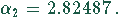
Diese Näherung ist schon ausreichend. Aus (1) errechnet sich die Höhe zu