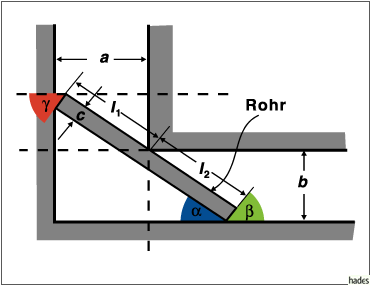
|
|
|
|
|
|
|
|
Aus einem Betrieb müssen Stahlrohre durch zwei rechtwinklig aufeinanderstoßende Straßen waagerecht um die Ecke transportiert werden.
Der Durchmesser des Rohres sei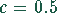 
m.
Die Straßenbreiten sind unterschiedlich (
m, 
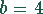m). Wie groß ist die
größte Länge des Rohres, das noch transportiert werden kann?
Lösung:
Aus der Abbildung sind folgende Zusammenhänge zu erkennen:
Da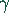 
und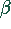 
Wechselwinkel sind, folgt
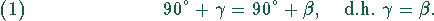
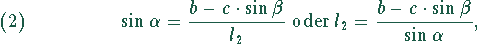
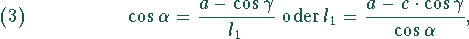
Zwischen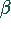 
und 
besteht der Zusammenhang
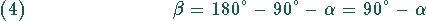
Damit ergibt sich aus (2) und (3)
und
Die Gesamtlänge des Rohres ist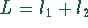 
. Daraus ensteht die auf einen
Extremwert zu untersuchende Funktion
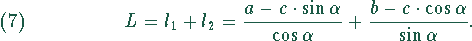
Damit ergibt sich
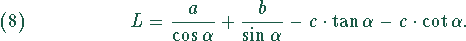
Für die Extremstelle muß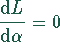 
sein.
Mit Hilfe der Quotientenregel ergibt sich
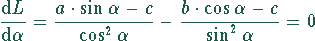
oder
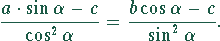
Durch Überkreuzmultiplikation erhält man die transzendente Gleichung
Mit den Zahlenwerten ergibt sich
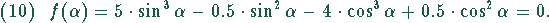
Transzendente Gleichungen lassen sich in der Regel nur numerisch lösen. Als Lösungsmethode soll das Newton-Verfahren verwendet werden.
Für die erste Näherung verwendet man zweckmäßigerweise die Lösung der Aufgabe
für ein Rohr mit verschwindendem Durchmesser (
).
Aus (9) folgt
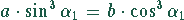
Da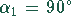 
keine Lösung des Problem sein kann, können wir dividieren
und erhalten
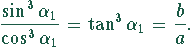
Das ergibt die Lösung
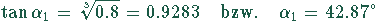
bzw. in Bogenmaß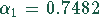 
.
Aus (10) folgt
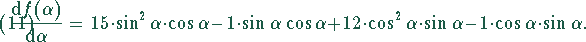
Damit läßt sich folgende Tabelle aufbauen
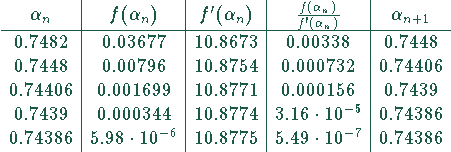
Als Lösung erhält man
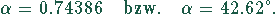
Mit diesem Wert können die Teillängen nach (5) und (6) berechnet werden:
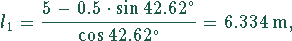
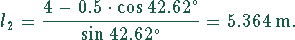
Die Gesamtlänge ergibt
