Komplexe Funktionen/Regelkreis

Der Frequenzgang eines offenen Regelkreises wird durch die komplexe Funktion

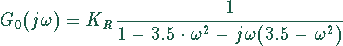
gegeben. Tragen Sie die Kurve in der komplexen Zahlenebene auf.

Lösung:

Man muß durch eine geeignete Umformung die Funktion in folgende Form bringen:

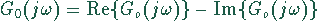
Das erreicht man durch Multiplikation mit 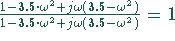. Dann ergibt sich

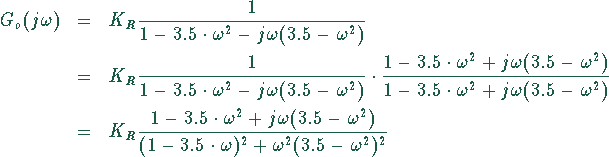
Daraus folgt für den Realteil

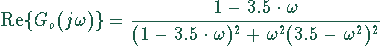
und für den Imaginärteil

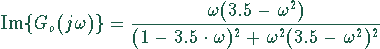
Trägt man diese Größen in der Gaußschen Zahlenebene als Funktion von auf, so ergibt sich die folgende Abbildung:

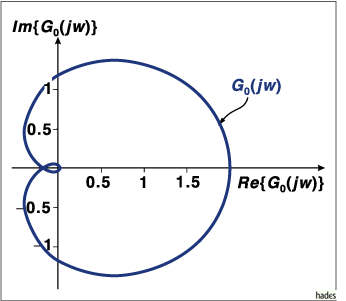
Diese Aufgabe läßt sich sehr gut mit Mathematica bzw. MapleV lösen.

Mathematica

f[t_]:=Re[2/(1-3.5 t^2-I t(3.5 -t^2))];
g[t_]:=Im[2/(1-3.5 t^2-I t(3.5 -t^2))]

ParametricPlot[{f[t],g[t]},{t,-5,5}]

MapleV

f(t):=2*(1-3.5*t^2)/((1-3.5*t^2)^2+t^2(3.5-t^2)^2);
g(t):=2*t(3.5-t^2)/((1-3.5*t^2)^2+t^2(3.5-t^2)^2);
plot([f(t),g(t),t=-5..5]);