






 |
 |
 |
 |
 |
 |
 |
Die Syntax lautet:
ConstrainedMax[Zielfunktion,{Einschränkungen in Form von Ungleichungen mit < =
bzw. > = },{Variable}]
(* oder *)
ConstrainedMin[ ]
Beispiel:
Es werden die Produkte 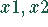 auf den Maschinen
auf den Maschinen 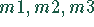 produziert. die
Gewinnfunktion ist
produziert. die
Gewinnfunktion ist
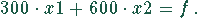
Die Produktionszeit/Monat auf den Maschinen beträgt:
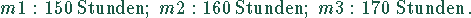
Das Produkt 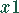 benötigt auf den Maschinen
benötigt auf den Maschinen 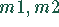 je 3 Stunden. Das Produkt
je 3 Stunden. Das Produkt
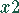 benötigt auf der Maschine
benötigt auf der Maschine 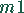 2 Stunden, auf der Maschine
2 Stunden, auf der Maschine 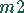 4 Stunden
und auf der Maschine
4 Stunden
und auf der Maschine 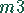 6 Stunden. Daraus ergibt sich folgende Optimierung:
6 Stunden. Daraus ergibt sich folgende Optimierung:
(* Beispiel *)
Remove["Global`*"]
f=300*x1+600*x2
einschr1=3*x1+2*x2<=150
einschr2=3*x1+4*x2<=160
einschr3=6*x2<=170
ConstrainedMax[f,{einschr1,einschr2,einschr3},{x1,x2}]
(* das erste Glied ist der erzeugte Gewinn *)
Ein Beispiel für Transportprobleme:
Ein Transportunternehmen hat drei Milchwerke (m1,m2,m3) mit Milch von drei Rinderställen (r1,r2,r3) zu beliefern. Der tägliche Bedarf beträgt 1000 l, 2000 l bzw. 2500 l. Die Rinderställe haben eine Tageskapazität von 800 l, 1500 l, 2300 l.
Die Transportkosten pro 1 Liter Milch in DM sind in der folgenden Tabelle aufgeführt:
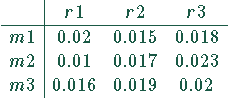
Die Gesamtkosten sollen minimiert werden.
Es existieren neun Variable (x[1][1], x[1][2] usw. bis x[3][3]), da jedes Milchwerk von jedem Rinderstall beliefert werden kann. Die zu minimierende Größe ist
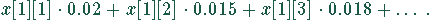
Die Einschränkungen sind einmal durch die Kapazität der Milchwerke gegeben:
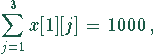
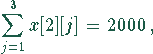
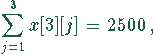
und zum anderen durch die Kapazität der Rinderställe bestimmt:
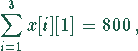
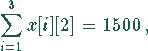
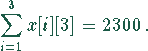
In Mathematica läßt sich dieses Problem wie folgt lösen:
Remove["Global`*"]
ri={1700,1500,2300}
mi={1000,2000,2500}
kosten={{0.02,0.015,0.018},{0.01,0.017,0.023},{0.016,0.019,0.02}}
r = Join[ Table[Sum[x[i][j],{j,1,3}]==ri[[i]],{i,1,3}],
Table[Sum[x[i][j],{i,1,3}]==mi[[j]],{j,1,3}]]
v=Flatten[Table[x[i][j],{i,1,3},{j,1,3}]]
z=Sum[x[i][j] * kosten[[i]][[j]],{i,1,3},{j,1,3}]
ConstrainedMin[z,r,v]
Dieses Beispiel kann leicht auf mehr Quellen und Zielorte erweitert werden.
