Residuensatz

Wegintegrale, bei denen der geschlossene Weg Unstetigkeitstellen einschließt, können mittels des Residuensatzes berechnet werden:

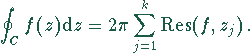
Dazu werden die Unstetigkeitsstellen benötigt. Ist 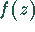eine rationale Funktion, dann können die Unstetigkeitsstellen durch Bestimmung der Nullstellen des Nenners berechnet werden.

Remove["Global`*"]
f=              (* Funktion eingeben *)
Solve[Denominator[f]==0,z]

Prüfung welche Nullstellen in dem Bereich des Wegintegrals liegen:

z1=            (* erste Nullstelle eingeben *)
z2=            (* zweite Nullstelle eingeben *)
Abs[z1]   //N
Abs[z2]  //N
(* In Abhängigkeit von der Zahl der Nullstellen *)

Damit kann mittels des Residuensatzes das Wegintegral bestimmt werden:

z1=           (* erste Unstetigkeitsstelle *)
z2=           (* zweite Unstetigkeitsstelle usw. *)
2 Pi (Residue[f,{z,z1}]+Residue[f,{z,z2}])  //N
(* je nachdem wieviel Unstetigkeitsstellen durch den Weg eingeschlossen
sind *)

Ist f keine rationale Funktion, so kann versucht werden, die Unstetigkeitstellen durch Bestimmung der Nullstellen der reziproken Funktion 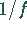zu finden.

Remove["Global`*"]
f=          (* Funktion eingeben *)
f1=1/f
Solve[f1==0,z]