|
|
|
|
|
|
|
|
können im Bereich 
doppeltlogarithmisch dargestellt werden,
d.h. mit einer logarithmischen Skalierung der x-Achse und der
y-Achse.
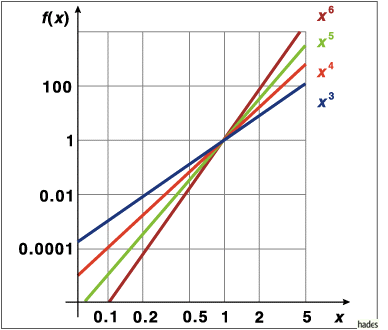
In doppeltlogarithmischer Darstellung sind die Graphen von 
Geraden, deren Steigung der Exponent n der Potenzfunktion ist.
Geraden gleicher Potenz, aber unterschiedlicher Vorfaktoren a,
haben gleiche Steigung, sind aber gegeneinander in y-Richtung
verschoben.
Geraden unterschiedlicher Potenz haben unterschiedliche Steigung.
Im Fall gleicher Vorfaktoren schneiden sie sich im Punkt (
).
Doppeltlogarithmische Regression: Eine Anpassung einer
Potenzfunktion 
an Datenpunkte (
)
kann mit Hilfe einer linearen Regression erfolgen, wenn hierzu
die logarithmierten Punkte 
eingelesen
werden.
Die bei der linearen Regression gewonnene Steigung a
beschreibt den Exponenten der Potenzfunktion und der y-Achsenabschnitt
b den Logarithmus des Vorfaktors 
.
|
|
|
|
|
|
|
|
