Nichtlineare Argumente

Sinus- und Cosinusfunktion - Nichtlineare Argumente

Eine nichtlineare Funktion von x im Argument verändert die Periode der Funktion in Abhängigkeit von x.
Ein Quadrat im Argument läßt die Funktion für größere x zunehmend schneller schwingen.

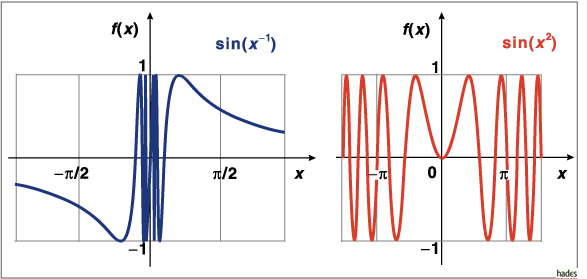
Ein Spezialfall ist die Funktion

Die Funktion schwingt für immer schneller. Am Punkt ist die Funktion nicht definiert und kann auch nicht stetig erweitert werden.

Mathematica Code:

f1=Plot[Sin[x^(-1)],{x,0.02 Pi,Pi},PlotRange->{{0.02 Pi,Pi},{-1.2,1.2}},
PlotStyle->{Hue[0]},AspectRatio->Automatic]

f2=Plot[Sin[x^(-1)],{x,-Pi,-0.02 Pi},PlotRange->{{-Pi,-0.02 Pi,},{-1.2,1.2}},
PlotStyle->{Hue[0]},AspectRatio->Automatic]

Show[{f1,f2}]

Dies ist ein Fall, in dem eine Funktion nicht stetig ist, obwohl sie weder divergiert noch Sprünge macht.

Multipliziert man die Funktion mit x, so wird die neue Funktion zwar im Punkt

durch

stetig erweiterbar, ist aber dort nicht differenzierbar.