|
|
|
|
|
|
|
|
Dieser Ast werde durch zwei Geraden 
und 
geschnitten
Der Schnittpunkt von g mit der Hyperbel hat die Komponenten
, wobei gemäß der Hyperbelgleichung
gilt und
das Vorzeichen durch das Vorzeichen von T bestimmt wird.
Die verdoppelte von 
mit der Hyperbel eingeschlossene
Fläche habe den Betrag 
.
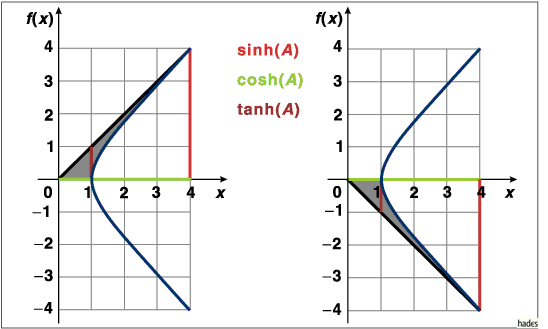
Gibt man dem Wert A das Vorzeichen von T (positiv, wenn g positive Steigung hat, negativ, wenn g negative Steigung hat), so lassen sich folgende Beziehungen zwischen A, C, S und T aufstellen:
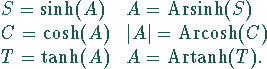
Die Funktionen Sinus hyperbolicus,
Cosinus hyperbolicus
und Tangens hyperbolicus
lassen sich geometrisch als y-Koordinate und x-Koordinate des
Schnittpunkts sowie als Geradensteigung bei einem Schnitt einer
Geraden mit der ,,Einheitshyperbel`` interpretieren.
Diese Interpretation
entspricht der Interpretation von Sinus, Cosinus und
Tangens bei dem
Schnitt einer Geraden mit einem Einheitskreis.
Aus diesem Zusammenhang lassen sich die genannten Funktionsnamen und
die Alternativnamen hyperbolischer Sinus, hyperbolischer
Cosinus und hyperbolischer Tangens wie auch die Bezeichnungen
hyperbolische Funktionen und Hyperbelfunktionen
verstehen.
Aus der geometrischen Beschreibung lassen sich die beiden
wichtigsten Umrechnungsregeln der hyperbolischen Funktionen
entnehmen,
|
|
|
|
|
|
|
|
