Hyperbolische Sinus- und Cosinusfunktion - Grafische Darstellung:
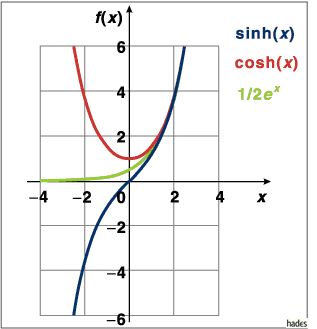
Mathematica Code:
Plot[{Sinh[x],Cosh[x],(1/2)Exp[x]},{x,-4,4},PlotRange->{{-4,4},{-6,6}},
PlotStyle->{{Hue[0]},{Hue[0.3]},{Hue[0.6]}},AspectRatio->Automatic]
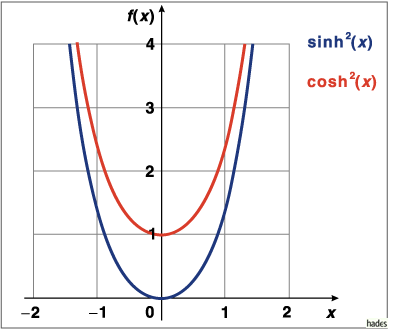
Mathematica Code:
Plot[{(Sinh[x])^2,(Cosh[x])^2},{x,-2,2},PlotRange->{{-2,2},{0,4}},
PlotStyle->{{Hue[0]},{Hue[0.3]}},AspectRatio->Automatic]
 Beide Funktionen wachsen mit großem x exponentiell ins Unendliche.
Beide Funktionen wachsen mit großem x exponentiell ins Unendliche.
Der Sinus hyperbolicus ist punktsymmetrisch zum Ursprung, hat bei  den Wert
den Wert
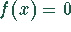 und geht für große negative Werte
und geht für große negative Werte 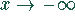 gegen
gegen
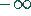 . Die Funktion läßt sich in der Nähe des Ursprungs durch
eine Gerade
. Die Funktion läßt sich in der Nähe des Ursprungs durch
eine Gerade  nähern.
nähern.
Der Cosinus hyperbolicus ist spiegelsymmetrisch zur y-Achse und hat ein Minimum
bei 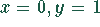 . Für große negative Werte
. Für große negative Werte 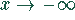 geht die
Funktion gegen
geht die
Funktion gegen 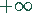 .
.
 Sinus hyperbolicus und Cosinus hyperbolicus nähern sich für große
positive Werte von x immer mehr aneinander an.
Sinus hyperbolicus und Cosinus hyperbolicus nähern sich für große
positive Werte von x immer mehr aneinander an.
Ein Faktor 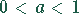 im Argument verbreitert die Kurven und verringert
die Steigung. Für
im Argument verbreitert die Kurven und verringert
die Steigung. Für 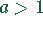 wird die Steigung größer und
die Figur schmaler.
wird die Steigung größer und
die Figur schmaler.
Negatives a läßt den Sinus hyperbolicus zu einer fallenden Funktion werden, der
Cosinus hyperbolicus ändert sich bei Vorzeichenänderung nicht.
Das Quadrat der Funktionen steigt für 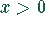 schnell an.
schnell an.
 Die
Funktionen
Die
Funktionen 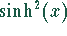 und
und 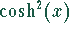 unterscheiden sich nur um
eine additive Konstante
unterscheiden sich nur um
eine additive Konstante 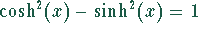 .
.

















 Beide Funktionen wachsen mit großem x exponentiell ins Unendliche.
Beide Funktionen wachsen mit großem x exponentiell ins Unendliche.
 Sinus hyperbolicus und Cosinus hyperbolicus nähern sich für große
positive Werte von x immer mehr aneinander an.
Sinus hyperbolicus und Cosinus hyperbolicus nähern sich für große
positive Werte von x immer mehr aneinander an.
 Die
Funktionen
Die
Funktionen 






