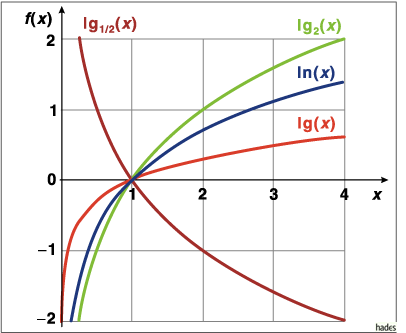
|
|
|
|
|
|
|
|
Mathematica Code:
Plot[{Log[x],Log[10,x],Log[2,x],Log[1/2,x]},{x,0.01,4}, PlotRange->{{-0.5,4.5},{-2,2}},
PlotStyle->{{Hue[0]},{Hue[0.3]},{Hue[0.6]},{Hue[0.8]}}, AspectRatio->Automatic]
Der natürliche Logarithmus steigt schneller als der dekadische Logarithmus und langsamer als der duale Logarithmus.
Logarithmen zu Zahlen 
fallen. Sie entsprechen den Logarithmen
der reziproken Argumente zur reziproken Basis.
|
|
|
|
|
|
|
|
