|
|
|
|
|
|
|
|
Schnitte parallel zur z-Achse sind Parabeln, dazu senkrechte Schnitte sind Ellipsen.
Rotationsparaboloid: für den Fall 
, durch Drehung der
Parabel
in der 
-Ebene um ihre Symmetrieachse.
Rauminhalt eines Teiles des Paraboloids bis zu einer zur z-Achse senkrechten Ebene in der Höhe h:
Schnitte senkrecht zur x- oder y-Achse sind deckungsgleiche Parabeln,
Schnitte senkrecht zur z-Achse sind Hyperbeln (und ein sich
schneidendes Geradenpaar für 
).
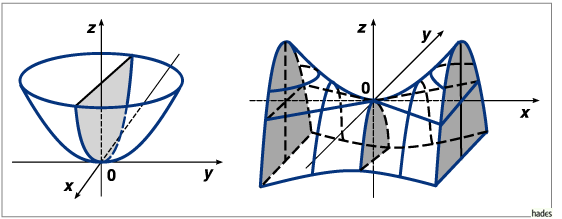
Elliptisches Paraboloid und hyperbolisches Paraboloid.
Geradlinige Erzeugende einer Fläche: Gerade, die ganz in der Fläche liegt.
Die zwei Scharen von Erzeugenden des hyperbolischen Paraboloids:
wobei u und v beliebige Größen sind. Durch jeden Flächenpunkt gehen jeweils zwei erzeugende Geraden hindurch.
|
|
|
|
|
|
|
|
