Mathematische Modellformulierung

Beide Produkte werden auf den Maschinen und bearbeitet. Produkt benötigt auf eine Bearbeitungszeit von h und auf h. benötigt auf h und auf h. Die wöchentlichen Maschinenlaufzeiten sind für auf h und für auf h begrenzt.

Gesucht ist ein optimales Wochenproduktionsprogramm , das den Reingewinn (unter Beachtung noch zu formulierender Nebenbedingungen) maximal macht.
 
Ziel- oder Zweckfunktion:    Lineare Funktion der Strukturvariablen.

Die Zielfunktion verknüpft die Strukturvariablen mit den Strukturkonstanten .
 
max. (Z.F.).
 
Die Suche des Minimums einer Zielfunktion z ist gleichbedeutend mit der Suche des Maximums von . Durch Multiplikation von z mit kann ein Minimierungsproblem also in eine Maximierungsaufgabe überführt werden und umgekehrt. Daher können Rechenprogramme, die die Zielfunktion maximieren (minimieren), auch zur Suche eines Minimums (Maximums) verwendet werden.
 
Nebenbedingungen ( Restriktionen):

 
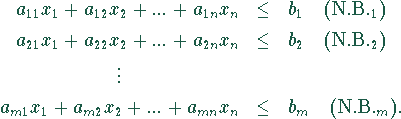
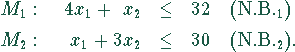
Nichtnegativitätsbedingungen: Allgemein wird gefordert, daß die Strukturvariablen nur Werte annehmen: .
 
Da keine negativen Produktionszahlen möglich sind, gelten zusätzlich zu den Nebenbedingungen die Nichtnegativitätsbedingungen:
 
Mathematisches Modell: Das Aufstellen der Zielfunktion, der Nebenbedingungen und der Nichtnegativitätsbedingungen.

Normalfall: Nebenbedingungen von Maximierungsmodellen enthalten nur -Beziehungen, diejenigen von Minimierungsmodellen dagegen nur -Beziehungen.
 
Enthalten einzelne Nebenbedingungen (anstatt ) das Ungleichheitszeichen , so können diese durch Multiplikation mit in Ungleichungen mit der Bedingung umgeformt werden, beziehungsweise umgekehrt.
 
Verallgemeinerter (erweiterter) Normalfall: Zusätzlich zu den Ungleichungen können auch lineare Gleichungen als Nebenbedingungen auftreten.