|
|
|
|
|
|
|
|
Setzt man in den Nebenbedingungen die Schlupfvariablen zu Null, so begrenzen die resultierenden Geraden zusammen mit den Nichtnegativitätsbedingungen den zulässigen Bereich, innerhalb dessen das Maximum der Zielfunktion liegen muß, es sei denn daß keine Optimierung existiert (unendliche Kanten).
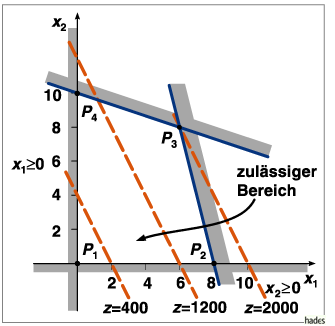
Anhand der eingezeichneten Linien mit konstantem Zielfunktionswert
konst. (Höhenlinien) wird deutlich, daß die Zielfunktion
eine ebene Fläche über der 
-Ebene darstellt. Das
Maximum der Zielfunktion kann somit nur in einem Eckpunkt (ausnahmsweise
auch auf einer Seite) des zulässigen Bereichs liegen. Daher genügt es,
nur die Eckpunkt auf ihre Zielfunktionswerte zu untersuchen.
Eckpunkt-Berechnungsmethode:
Bestimme alle Eckpunkte (Schnittpunkte von jeweils zwei begrenzenden
Geraden) des Polyeders und setze diese Wertepaare in die
Zielfunktion ein.
Der maximale Wert von z entspricht dem Maximum der Zielfunktion.
Ergebnis: 
DM für 
und 
.
Eine lineare Optimierungsaufgabe hat in mindestens einem
Eckpunkt ein Maximum oder Minimum. Existieren mehrere Eckpunkte des
Polyeders mit maximalem oder minimalem Zielfunktionswert, so ist
das Maximum oder Minimum in der gesamten ebenen Fläche, die
durch diese Punkte festgelegt ist, gegeben.
Mehrere optimale Lösungen treten auf, wenn die Steigung
der Höhenlinien der Zielfunktion gleich der Steigung
einer Begrenzungsgeraden ist.
|
|
|
|
|
|
|
|
