|
|
|
|
|
|
|
|
oder 
über die
Regel von Bernoulli und de l'Hospital:
Gilt
so läßt sich der Grenzwert des Quotienten der Funktion (sofern er existiert) als Grenzwert der Quotienten der ersten Ableitungen schreiben:
Nenner und Zähler sind jeweils getrennt abzuleiten. Nicht
den Bruch mit der Quotientenregel ableiten!
Die Regel gilt auch für rechts- bzw. linksseitige Grenzwerte,
falls
Die Regel läßt sich häufig auch auf Folgen der Form
anwenden, wenn Zähler-
und Nennerfolge gegen 0 (oder 
) konvergieren und sich in der Form
mit auf 
definierten differenzierbaren Funktionen schreiben lassen.
Man ersetze dann den Index durch die reelle Zahl 
und bilde den
Grenzwert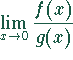 
unter
Zuhilfenahme der Regel von l'Hospital.
Ergibt sich nach Anwendung der Regel wieder eine unbestimmte Form, kann
die Regel mehrmals angewendet werden, falls die Voraussetzungen für
die Ableitungen erneut gegeben sind.
,
die Exponentialfunktion strebt schneller gegen unendlich als
jede Potenzfunktion.
Unter Umständen erreicht man mit dieser Regel keine Grenzwertbestimmung,
obwohl ein Grenzwert vorhanden ist.
|
|
|
|
|
|
|
|
