Wegeunabhängigkeit der komplexen Integration

Sei eine glatte Kurve C in einem einfach zusammenhängenden Gebiet gegeben. Ist
eine auf G stetige Funktion, dann ist das Kurvenintegral

dann und nur dann vom speziellen Verlauf der Kurve C unabhängig, wenn f analytisch in G ist.
 
Zur Berechnung des Integrals kann man sich den Integrationsweg wählen, der die Berechnung erleichtert.

In der folgenden Abbildung sind einfach und mehrfach zusammenhängende Gebiete dargestellt:

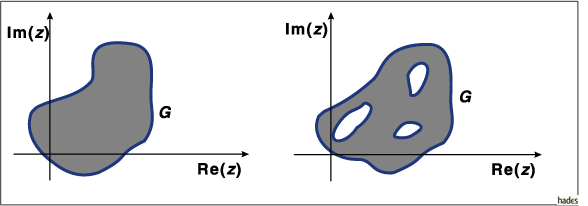
Dieser Satz bildet die Grundlage für den Cauchyschen Integralsatz.