Hebbare Singularität
Hebbare Singularität,
isolierte Singularität a der Funktion f, in deren
Umgebung die Laurentreihe von f keine negativen Potenzen von 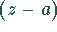 enthält
enthält 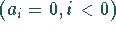 .
.
In diesem Fall
existiert der Grenzwert  . Aus der
Laurentreihenentwicklung entnimmt man
. Aus der
Laurentreihenentwicklung entnimmt man
 . Man betrachtet diese Gleichung als Definition
für den Funktionswert von f im Punkt a. Damit
wird die Funktion analytisch in a, a ein
regulärer Punkt, und die Singularität behoben.
. Man betrachtet diese Gleichung als Definition
für den Funktionswert von f im Punkt a. Damit
wird die Funktion analytisch in a, a ein
regulärer Punkt, und die Singularität behoben.
 Die Funktion
Die Funktion  ist nicht definiert für
ist nicht definiert für  .
Jedoch ist die Laurentreihe
.
Jedoch ist die Laurentreihe
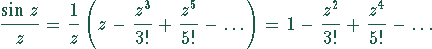
und folglich 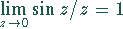 .
Mit der Definition
.
Mit der Definition 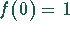 wird die Singularität bei
wird die Singularität bei  behoben.
behoben.















 Die Funktion
Die Funktion ![]()
![]() .
Mit der Definition
.
Mit der Definition ![]() wird die Singularität bei
wird die Singularität bei ![]() behoben.
behoben.






