Euler-Verfahren

Annäherung der Ableitung durch den Differenzenquotienten für explizite Differentialgleichungen erster Ordnung.

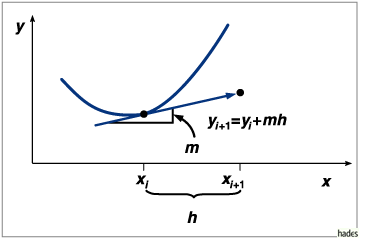
Euler-Verfahren, h: Schrittweite, m: Steigung

Geometrische Interpretation, der neue Funktionswert wird durch die Tangente im alten Funktionswert angenähert.

Fehler der Näherung, , eine infinitesimale Größe der Ordnung h, d.h. proportional zur Schrittweite h.

Beginne mit der Anfangsbedingung und berechne die nachfolgenden Funktionswerte gemäß obiger Gleichung.

Schrittweite h, kann fortwährend halbiert werden, bis

Vorteil, das Verfahren ist schnell und einfach zu programmieren.

Nachteil, das Verfahren ist nicht sehr zuverlässig.
 
Eulers Verfahren kann leicht gegen ein falsches Ergebnis laufen!