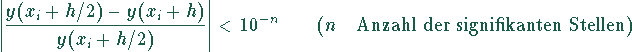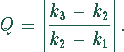Schrittweitenanpassung

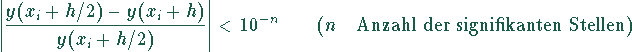
oder man wählt einen festen Wert vor.

Schrittweitenanpassung für das Runge-Kutta-Verfahren 4. Ordnung

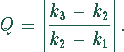
Ist die Schrittweite zu groß, so liegt die gewählte Näherung zu weit von der ,,wahren`` Lösung entfernt, und man entfernt sich mit zunehmender Rechnung immer weiter davon. Daher sollte Q<0,1 sein. Andererseits darf die Schrittweite nicht zu klein sein, da sich sonst die Rundungsfehler zu stark aufsummieren, d.h. es sollte Q>0,025 sein. Algorithmus zur Bestimmung der optimalen Schrittweite:

1. Beginne den ersten Rechenschritt mit der vorgewählten Schrittweite h.
2. Berechne den Faktor Q.
3. Falls Q>0,1 ist, setze 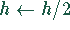und wiederhole den letzten Schritt.
4. Falls Q<0,025 ist, akzeptiere die berechnete Näherung, aber setze im nächsten Schritt .
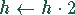5. Falls 0,025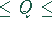0,1 ist, fahre mit derselben Schrittweite fort.