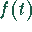|
|
|
|
|
|
|
|
, multipliziert mit 
, vermindert um ein Polynom 
-ten
Grades in der Variablen s. 
-ten Grades
Die Koeffizienten des Polynoms sind die
Anfangswerte (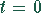
) der Originalfunktion und nacheinander ihrer
Ableitungen, wobei im letzten Koeffizienten die (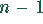
)-te Ableitung
steht:
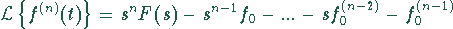
mit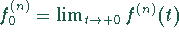 
.
Der obere eingeklammerte Index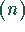 
an der Funktion f bezeichnet ihre n-te Ableitung.
Der Differentiationssatz ist der zentrale Satz, der es
erlaubt,
Differentialgleichungen (Differentiation im Originalbereich)
in algebraische Gleichungen (Multiplikation im Bildbereich)
transformieren zu können.
|
|
|
|
|
|
|
|
