|
|
|
|
|
|
|
|
Ein zweimaliges Werfen mit einem Würfel ergibt ein Ziffernpaar
aus der Menge aller möglichen Ziffernpaare
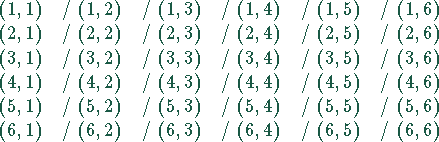
Das Ereignis 
soll genau dann eingetroffen sein,
wenn eine der beiden gewürfelten Ziffern in der Menge 
enthalten ist.
So ist es möglich, daß zwei
Ereignisse, z.B. 
, gleichzeitig eintreffen
können. Die Gesamtanzahl der möglichen Ereignisse ist genau
. Die Wahrscheinlichkeit,
ein Element aus der Ereignisuntermenge 
zu
würfeln, ist daher
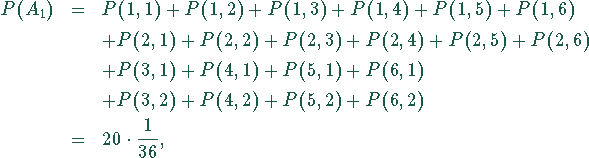
da die Wahrscheinlichkeit des Elementarereignisses 
ist.
Analog sind ebenso 
und 
.
Die Wahrscheinlichkeit 
, daß das
Würfelergebnis in 
und in 
liegt, errechnet sich
nach dem Multiplikationssatz zu
vorausgesetzt, 
sei bereits erfüllt worden, d.h. 
ist bereits ein Element der Menge 
. Dann ist
die Wahrscheinlichkeit 
dafür, daß
unter den insgesamt 20 Ereignissen
aus 
genau diejenigen gewürfelt wurden, die auch
in der Menge 
enthalten sind,
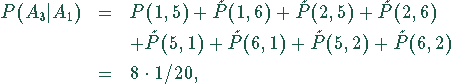
denn die Wahrscheinlichkeit für das Elementarereignis
mit 
aus 
ist in diesem Fall
.
Daraus folgt
Rechnet man das explizit nach, ergibt sich das richtige Ergebnis
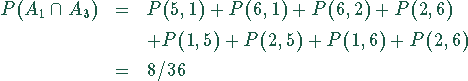
Die Wahrscheinlichkeit 
, daß das
Würfelergebnis in 
oder in 
liegt, errechnet sich
nach dem Additionssatz zu
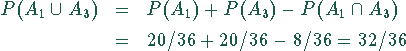
Das ist richtig, da nur die vier Ereignisse
und 
nicht zu den Mengen 
und 
gehören.
|
|
|
|
|
|
|
|
