Arbeitsweise

Arbeitsweise

Der Zustand jedes Knotens ergibt sich aus den Signalen, die er von anderen Knoten erhält. Jeder Verbindung zwischen zwei Knoten (in der Biologie: Synapse) ist ein Verbindungs-Gewicht zugeordnet. Ein darüber weitergegebenes Signal wird mit dem entsprechenden Gewicht multipliziert. Jeder Knoten addiert in der Regel alle eingehenden Signale und wendet auf die Summe eine einfache Funktion an. Sie hat meist S-förmige Gestalt und wird deshalb auch Sigmoidfunktion genannt.

Eine der gängigsten Sigmoidfunktionen ist der Tangens hyperbolicus.

Das Ergebnis kann unmittelbar als eigenes Signal weitergegeben werden. Meist hat jede Verbindung von einem Knoten j zu einem Knoten i ein eigenes Gewicht

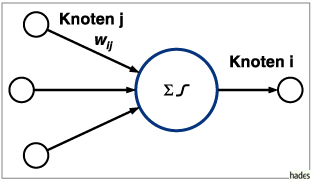
Technisches Modell eines Neurons

Die Gewichte bestimmen die Reaktion eines Netzes auf eine Eingabe und sind damit sein Informationsspeicher.

Die Nichtlinearität von Sigmoidfunktionen ist entscheidend für die Leistungsfähigkeit von neuronalen Netzen. Differenzierbarkeit, streng monotones Verhalten und Beschränktheit sind aus mathematischen Gründen notwendig bzw. sinnvoll.

Es erweist sich als günstig, Schwellenparameter einzuführen, die das Argument der Sigmoidfunktionen verschieben. Man behandelt die Schwellenparameter wie Gewichte für Verbindungen, die von einem Knoten mit konstantem Signal (meist ) ausgehen.

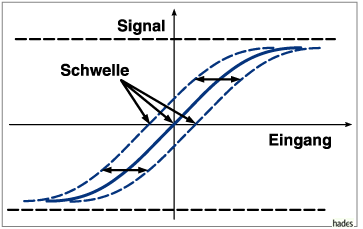
Wirkung einer Sigmoidfunktion bei verschiedenen Werten des Schwellenparameters

Lernen: Neuronale Netze lernen aus Beispiel-Eingaben mit oder ohne Beurteilung ihrer jeweiligen Ausgaben ( überwachtes bzw. unüberwachtes Lernen), indem sie ihre Gewichte verändern.

Bei vielen Lernverfahren ist es sinnvoll, die Gewichte vor Beginn des Lernens mit (kleinen) Zufallswerten zu belegen.