






 |
 |
 |
 |
 |
 |
 |
Der Bruch  sollte gekürzt werden. Ein Schüler kürzte kühn, indem
er einfach die gleichen Ziffern im Zähler und Nenner strich. Er hatte Glück.
Das Ergebnis war richtig.
sollte gekürzt werden. Ein Schüler kürzte kühn, indem
er einfach die gleichen Ziffern im Zähler und Nenner strich. Er hatte Glück.
Das Ergebnis war richtig.
Gibt es noch andere Brüche mit zweistelligen Zählern und Nennern, bei denen das gleiche Verfahren zum Ziel führt?
Lösung:
Der allgemeine Ausdruck für einen solchen Bruch lautet
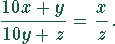
Dabei sind 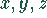 natürliche Zahlen mit den Bedingungen
natürliche Zahlen mit den Bedingungen
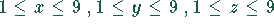 .
Daraus folgt
.
Daraus folgt
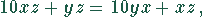
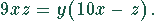
Die linke Seite der Gleichung erhält den Faktor 9. Deshalb muß die rechte
Seite durch 9 teilbar sein. Das bedeutet, entweder ist y oder 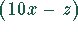 durch 9 oder sind beide zugleich durch 3 teilbar.
Daraus folgt: für y kommen nur die Zahlen 3, 6 und 9 in Frage.
durch 9 oder sind beide zugleich durch 3 teilbar.
Daraus folgt: für y kommen nur die Zahlen 3, 6 und 9 in Frage.
Fall 1:
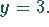 In diesem Fall ergibt sich die Gleichung
In diesem Fall ergibt sich die Gleichung
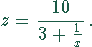
Nur für  existiert eine ganzzahlige Lösung für z, nämlich
existiert eine ganzzahlige Lösung für z, nämlich
 . Damit sind alle drei Unbekannten gleich:
. Damit sind alle drei Unbekannten gleich: 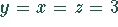 . Diese
Lösung ist trivial.
. Diese
Lösung ist trivial.
Fall 2: 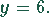 Für diesen Fall folgt
Für diesen Fall folgt
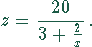
Für 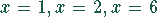 existieren ganzzahlige Lösungen für z. Wieder ergibt
existieren ganzzahlige Lösungen für z. Wieder ergibt
 die triviale Lösung:
die triviale Lösung: 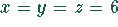 .
.
Für  ergibt sich
ergibt sich  , und
für
, und
für  folgt
folgt  .
.
Fall 3:
Für 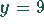 gilt die Gleichung
gilt die Gleichung
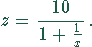
Für  und
und  existieren ganzzahlige Lösungen:
existieren ganzzahlige Lösungen:
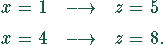
Es ist nun nur noch der Fall zu diskutieren, daß 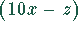 durch 9 teilbar
ist. Es gilt
durch 9 teilbar
ist. Es gilt
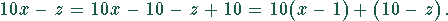
Aus den Teilbarkeitsregeln folgt:
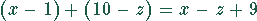
muß durch 9 teilbar sein. Das trifft aber nur auf  zu.
Das führt aber wieder zur Trivialität
zu.
Das führt aber wieder zur Trivialität 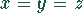 .
Es gibt deshalb außer dem Bruch
.
Es gibt deshalb außer dem Bruch  noch drei weitere Brüche
mit den gesuchten Eigenschaften
noch drei weitere Brüche
mit den gesuchten Eigenschaften
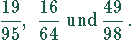
Natürlich gilt das auch für die reziproken Werte dieser Brüche.
