






 |
 |
 |
 |
 |
 |
 |
Es ist eine Lösung der Gleichung
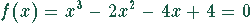
zu finden.
Eine ganzzahlige Lösung existiert nicht. Die Lösung soll auf drei Dezimalstellen
nach dem Komma genau ermittelt werden. Wir verwenden als Methode die
Intervallschachtelung, als Regula falsi bekannt.
Eine Nullstelle liegt zwischen 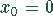 und
und 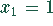 , denn
, denn 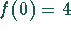 und
und 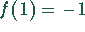 .
Zwischen den Werten
.
Zwischen den Werten 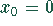 und
und 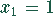 wechselt die Funktion
wechselt die Funktion 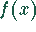 ihr Vorzeichen. Wegen der Übersichtlichkeit verwenden wir eine Tabelle
ihr Vorzeichen. Wegen der Übersichtlichkeit verwenden wir eine Tabelle
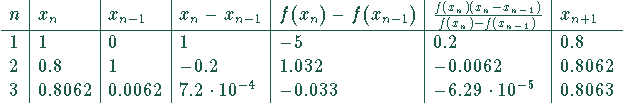
Damit ist es möglich, in der Funktion 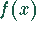 den Faktor
den Faktor 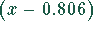 auszuklammern.
Das kann mit Hilfe des Horner-Schemas erfolgen.
auszuklammern.
Das kann mit Hilfe des Horner-Schemas erfolgen.
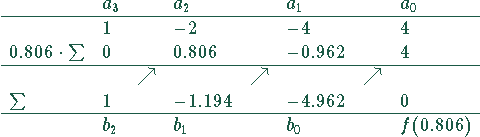
Damit ergibt sich
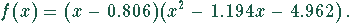
Die zweite Klammer ist eine quadratische Gleichung und kann nach dem üblichen Verfahren für quadratische Gleichungen gelöst werden.
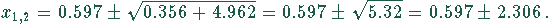
Die Lösungen sind also
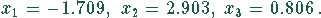
Mathematica
NSolve[x^3-2 x^2-4 x+4==0,x]
MapleV
solve(x^3-2.0*x^2-4*x+4=0,x);
Achtung! MapleV liefert für 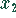 einen ganz geringen imaginären Anteil. Das ist ein
Rundungsfehler.
Bei Mathematica sind alle Lösungen reell.
einen ganz geringen imaginären Anteil. Das ist ein
Rundungsfehler.
Bei Mathematica sind alle Lösungen reell.
