|
|
|
|
|
|
|
|
In der Rentenrechnung spricht man von vorschüssiger Rente,
wenn die Renten jeweils zu Beginn der Perioden, z.B. des Jahres, gezahlt werden.
Der Rentenendwert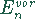 
ist derjenige Betrag, der zum Zeitpunkt
n ein Äquivalent für die n zu zahlenden Rentenbeträge darstellt.
Dies ist eine geometrische Reihe
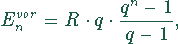
mit R der Rentenauszahlung und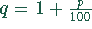 
dem Aufzinsfaktor. Dabei
ist p der Zinswert pro Periode (z.B. Jahr).
Der Rentenbarwer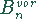t 
entspricht einem auf Zinseszins angelegten Kapitalbetrag, der
eine n-malige vorschüssige Rentenanzahlung ermöglicht, wobei das Kapital aufgebraucht
wird. Er beträgt
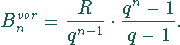
Von einer ewigen Rente spricht man, wenn die Rentenzahlung zeitlich
nicht begrenzt ist. Dies wird dann möglich, wenn die Rente nicht höher als die zu
jedem Zinstermin anfallenden Zinsen sind. Der vorschüssige Rentenbarwert der
ewigen Rente ist der Grenzwert der geometrischen Folge, die die Rentenbarwerte
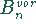bilden,
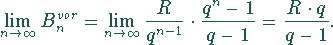
Die Rentenbarwerte bilden eine konvergente geometrische Folge.
