|
|
|
|
|
|
|
|
Ein Betrieb erhält den Auftrag, 19600 Stück eines Erzeugnisses herzustellen. In der ersten Woche (5 Arbeitstage) werden täglich 90 Stück produziert. Die produzierte Stückzahl/Woche ist bis zur Erfüllung des Auftrages um 50/Woche zu erhöhen.
Nach wieviel Wochen ist der Auftrag erfüllt?
Die Produktionszahlen pro Woche bilden eine arithmetische Folge, da sie konstant anwachsen. Die Werte der Folge genügen dem Gesetz:
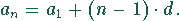
Dabei ist 
der Ausgangswert (Stückzahl/Woche) und d die konstante Differenzenfolge.
Die erreichte Stückzahl nach n Wochen errechnet sich
aus der Formel für eine arithmetische Reihe:
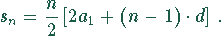
Gegeben:
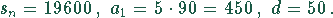
Lösung:
Die Größe n gibt die Anzahl der Wochen an, die benötigt werden, um die 19600 Stück zu produzieren. Durch Umstellen der obigen Gleichung für die arithmetische Reihe nach n ergibt sich
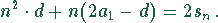
Mit den Zahlenwerten erhält man die Gleichung
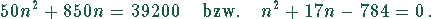
Dies ist eine quadratische Gleichung.
Mittels der Programme Mathematica oder MapleV kann man diese Gleichung leicht lösen.
In der Befehlszeile von Mathematica ist einzutragen:
NSolve[n^2+17 n-784 == 0, n]
Das Ergebnis von Mathematica lautet
In der Befehlszeile von MapleV ist einzutragen:
solve(x^2+17.0*x-784);
Durch Eingabe der 17 als rationale Zahl (17.0) wird die Lösung als Fließkommazahl ausgegeben.
In MapleV erhält man
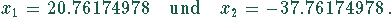
Die negativen Lösungswerte besitzen ökonomisch keine Bedeutung.
In der 21. Woche ist der Auftrag erfüllt. Nach 20 Wochen wurden
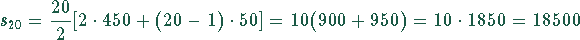
hergestellt.
In der 21.Woche brauchen deshalb nur noch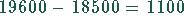 
Stück hergestellt
werden. Die in der 21. Woche hergestellte Stückzahl errechnet sich aus
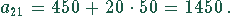
Bei einer gleichmäßigen Verteilung der Produktion auf die 5 Arbeitstage
werden in der 21. Woche nur 3.79 Tage für die Herstellung
der noch 1100 Stück benötigt.
