|
|
|
|
|
|
|
|
Ein Betrieb erhält den Auftrag, innerhalb eines Jahres 18258 Stück eines Erzeugnisses zu liefern. Die gegenwärtige Produktion liefert von diesem Erzeugnis 1400 Stück im Monat.
Wie muß die Arbeitsproduktivität monatlich gesteigert werden, damit der Auftrag erfüllt wird?
Die monatlich produzierte Stückzahl bildet offensichtlich eine geometrische Folge. Die im k-ten Monat produzierte Stückzahl errechnet sich aus
Die Summe der erzeugten Produkte nach k Monaten ergibt sich aus der geometrischen Reihe
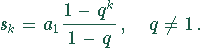
Gegeben:
Lösung:
Gesucht ist der Quotient q von zwei aufeinanderfolgenden Folgengliedern. Die Ausgangsgleichung bildet die geometrische Reihe
Durch Umstellen nach q ergibt sich eine Gleichung 12. Grades
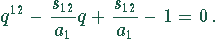
Zur Lösung dieser Gleichung kann Mathematica oder MapleV verwendet werden.
In der Befehlszeile von Mathematica ist einzutragen:
NSolve[q^(12)-(18258/1400) q+(18258/1400)-1 == 0,q]Die komplexen Lösungen haben ökonomisch keine Bedeutung. Die reelle Lösung
hat ebenfalls keine ökonomische Bedeutung,
da ein Einsetzen
in die Formel für die geometrische Reihe einen Bruch 
ergibt.
Das bedeutet, bei beliebigen Werten von 
und 
wird die Gleichung
12. Grades für 
erfüllt.
Es bleibt die Lösung 
In der Befehlszeile von MapleV ist einzutragen:
> fsolve(q^(12)-(18258/1400)*q+(18258/1400)-1,q);
Durch das Fehlen des Arguments complex werden die komplexen Werte in
MapleV unterdrückt.
Man erhält 
.
Ansonsten gilt das oben bei Mathematica Gesagte.
Als einzige ökonomisch vernünftige Lösung bleibt 
. Das bedeutet,
eine Steigerung von 1.5 % pro Monat ist erforderlich, um den Auftrag
termingemäß zu erfüllen.
