|
|
|
|
|
|
|
|
Der kürzeste Abstand eines Gebäudes von einer schnurgeraden Straße, die von der nächsten Stadt an dem Gebäude vorbeiführt, beträgt 20 km. Die Entfernung des Schnittpunktes der Senkrechten von dem Gebäude zur Straße von der Stadt beträgt 60 km.
Ein Fahrzeug der schnellen Hilfe soll in möglichst kurzer Zeit von der Stadt
zu dem Haus gelangen. An welcher Stelle der Straße muß es abbiegen?
(Die Geschwindigkeit auf der Straße ist 
km/h und im Gelände 
km/h.)
Lösung:
Es ist zweckmäßig sich eine Skizze anzufertigen.
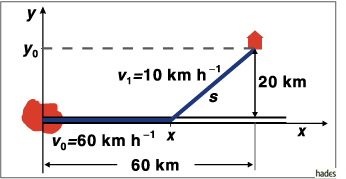
Man legt die x-Achse entlang der Straße. Die Zeit, die das Fahrzeug bis um
Punkt x zurücklegt, ist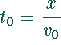 
. Für die restliche
Strecke benötigt es die Zeit
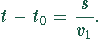
Die Strecke s kann mittels des Pythagoras errechnet werden:
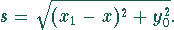
Setzt man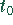 
ein und stellt nach t um, so ergibt sich
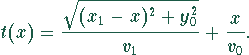
Die Variable ist x. Gesucht ist das Minimum der Funktion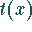 
.
Diese Funktion ist im Bereich 
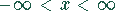definiert und stetig.
Sie besitzt keine Nullstellen.
Das Minimum erhält man durch Nullsetzen der ersten Ableitung
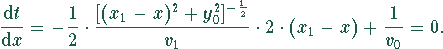
Durch Umformung folgt
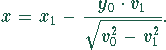
Mit den Zahlenwerten ergibt sich:
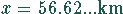
Diese Aufgabe kann auch mit den Mathematikprogrammen Mathematica und MapleV gelöst werden.
Mathematica
y=D[Sqrt[(60.-x)^2+400.]/10+x/60,x] Solve[y==0,x]
MapleV
y:=diff(sqrt((60-x)^2+400.)/10+x/60;x); solve(y=0,x);
