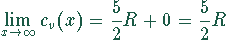|
|
|
|
|
|
|
|
Die molare Wärmekapazität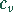 
eines zweiatomigen idealen Gases
bei konstantem Volumen v ist durch
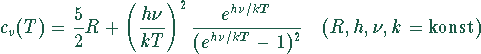
gegeben.
Wie verhält sich die molare Wärmekapazität bei sehr großen Temperaturen (
)
und bei sehr kleinen Temperaturen (
)?
Lösung:
Durch eine Substitution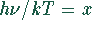 
wird die ganze Rechnung übersichtlicher.
Aus 
folgt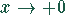 
, aus 
folgt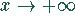 
. Damit ergibt sich die
Aufgabe für große Temperaturen
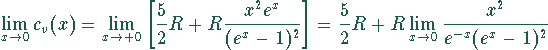
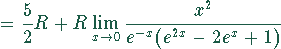
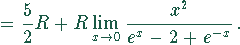
Bei dem Grenzübergang 
gehen sowohl der Zähler als auch der Nenner
gegen Null. Deshalb muß der Grenzübergang mittels der Regel von l'Hospital
berechnet werden.
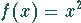
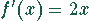
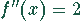
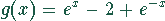
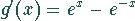
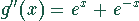
Auch nach der ersten Ableitung werden Nenner und Zähler beim Grenzübergang
Null. Darum muß noch die zweite Ableitung gebildet werden. Damit ergibt sich
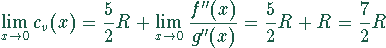
für große Temperaturen.
Analog erhält man
für kleine Temperaturen.
