|
|
|
|
|
|
|
|
Steht der Term im Nenner,
geht die Funktion für große 
-Werte gegen null.
Im Fall von ganzrationalen Funktionen gleichen Grades läuft
die gesamte Funktion gegen einen konstanten Wert (parallel zur x-Achse),
der gleich dem Quotienten der beiden Vorfaktoren der höchsten Terme
ist.
Man zerlege die gebrochenrationale Funktion
in eine echt gebrochene und in eine
ganzrationale Funktion, die Grenzkurve oder Asymptote.
Für große x-Werte nähert sich die Funktion der
Grenzkurve.
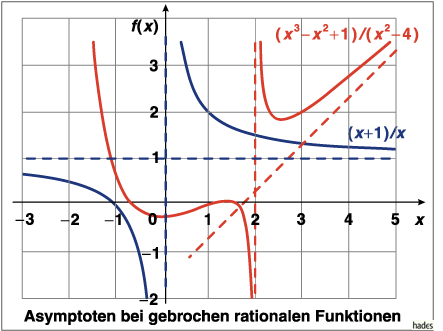
Zur Demonstration siehe nachfolgendes Bild:
|
|
|
|
|
|
|
|
