|
|
|
|
|
|
|
|
Ein zylindrisches Gefäß mit dem Volumen V soll mit minimalem Materialaufwand hergestellt werden. Die Wanddicke ist überall a.
Lösung:
Das Volumen des Gefäßes errechnet sich nach der Beziehung
Dabei ist h die Höhe des Gefäßes.
Der Materialaufwand ergibt sich aus
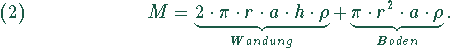
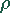ist die Dichte des verwendeten Materials.
Die Formel (1) kann man nach h auflösen und damit h aus (2) eliminieren
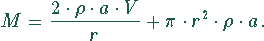
Den Wert für r, bei dem der Materialaufwand ein Minimum wird,
erhält man, wenn die erste Ableitung von
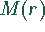Null gesetzt wird.
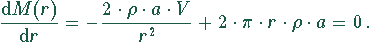
Für r ergibt sich
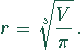
Zur Lösung kann sowohl Mathematica als auch MapleV verwendet werden.
Mathematica
y=D[(2 Pi ro a V)/r+Pi r^2 ro a,r] Solve[y==0,r]
MapleV
y:=diff((2*Pi*ro*a*V)/r+Pi*r^2*ro*a,r] solve[y=0,r]
