|
|
|
|
|
|
|
|
Ermitteln Sie die Lösungsmenge der Gleichung
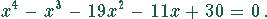
Lösung:
Zuerst prüft man die Teiler von 30, ob sie einer Lösung genügen. Teiler sind
(1, 2, 3, 4, 5, 6, 10, 15). Man findet das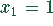 
eine Lösung der obigen Gleichung ist.
Mittels des Horner-Schemas läßt sich der Faktor 
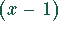aus der
Gleichung herausziehen
Das ergibt
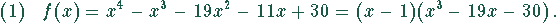
Der Teiler 2 liefert für die zweite Klammer keine Lösung, aber der Teile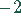r 
. Wieder kann mit Hilfe
des Horner-Schemas der Faktor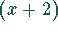 
ausgeklammert werden:
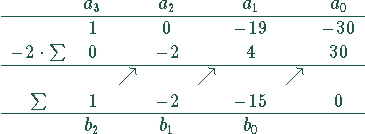
Damit wird aus (1)
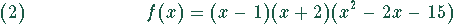
Die dritte Klammer in (2) ist eine quadratische Gleichung, die nach dem üblichen Verfahren für quadratische Gleichungen gelöst werden kann.
Die Lösungen sind
Wir erhalten also die Lösungsmenge
Damit kann das Polynom faktorisiert werden:
Mathematica
NSolve[x^4-x^3-19x^2-11x+30==0,x]
MapleV
> solve(x^4-x^3-19*x^2-11*x+30=0,x);
