|
|
|
|
|
|
|
|
Eine Messung lieferte folgende Wertetabelle
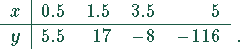
Zwischenwerte können durch eine Interpolation berechnet werden. Auf Grund der geringen Stützstellenzahl kann ein Lagrange-Polynom oder ein Newtonsches Polynom für die Interpolation verwendet werden. Bestimmen Sie die Polynome dritten Grades nach beiden Verfahren.
Lösung:
Es gilt
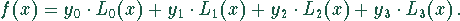
Für die Koeffizienten erhält man
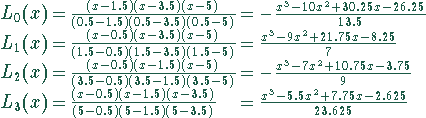
Damit ergeben sich für die einzelnen Summanden
Die Addition dieser Summanden ergibt
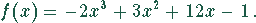
Das Interpolationspolynom nach Newton ist dritten Grades und lautet
Die Koeffizienten können schematisch berechnet werden
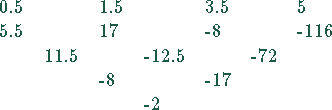
Damit werden die Koeffizienten
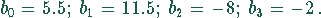
Das Newtonsche Interpolationspolynom lautet:
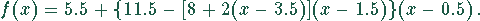
Bei den Interpolationsaufgaben sind Mathematikprogramme wie Mathematica oder MapleV besonders nützlich.
Mathematica
y:=InterpolatingPolynomial[{{0.5,5.5},{1.5,17},
{3.5,-8},{5,-116}},x]
Expand[y]
MapleV
interp([0.5,1.5,3.5,5.5],[5.5,17,-8,-116],x);
Mathematica benutzt dabei das Newtonverfahren.
