|
|
|
|
|
|
|
|
Es soll die optimale Losgröße eines Erzeugnisses bestimmt werden. Dabei ist ein Los eine begrenzte Anzahl konstruktiv gleichartiger Teile, die in einem Arbeitsgang bei einer einmaligen Vorbereitungs- und Abschlußzeit in zusammenhängender Folge gefertigt werden.
Die Losgröße beeinflußt einerseits die Selbstkosten je Stück. Sie sinkt mit wachsender Losgröße. Andererseits hat die Losgröße Einfluß auf die Lagerkosten, die für das je Los bereitzustellende Material mit steigender Losgröße wachsen.
Lösung:
Gegeben:
Die Entstehungskosten für ein Los sei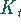 
. Sie setzen sich aus den Kosten
für die Vorbereitung und den Abschluß eines Loses 
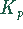und den Lagerkosten
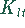für ein Los zusammen. Im Durchschnitt müssen für eine Zeit t (der
Zeit für die Abarbeitung eines Loses)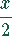 
Erzeugnisse gelagert werden.
Damit ergibt sich für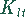 
Die Gesamtkosten eines Loses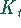 
sind dann
Für die Anzahl n Lose im Produktionszeitraum T und der Zeit t für die Abbarbeitung eines Loses gilt
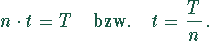
Analog gilt für das Produktionsvolumen Q:
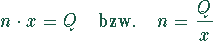
Damit ergibt sich für die Abarbeitungszeit eines Loses
Die Kostenfunktion in Abhängigkeit von der Losgröße erhält man, indem (2) mit der Anzahl n der Lose multipliziert wird
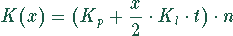
Mit den Werten für n und t ergibt sich
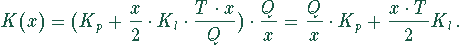
Für ein Minimum der Kosten muß die erste Ableitung gleich Null werden.
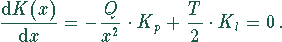
Die Lösung dieser Gleichung ergibt die optimale Losgröße
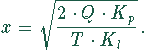
Die negative Lösung ist ökonomisch unrelevant.
Zur Bestimmung der Art des Extremwertes benutzt man die zweite Ableitung. Sie lautet:
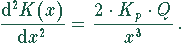
Sie ist für alle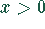 
größer Null. Die optimale Losgröße liefert
tatsächlich ein Minimum in der Kostenfunktion.
Mathematica
y=D[(KP+(x/2.) Kl (T x)/Q) (Q/x),x] Solve[y==0,x]
MapleV
y:=diff((KP+(x/2.)*Kl*T*x/Q)*Q/x,x); solve(y=0,x);
