|
|
|
|
|
|
|
|
In einem Unternehmen wurde die funktionelle Abhängigkeit zwischen
Ertrag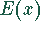 
und Produktionsmenge x zu
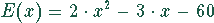
bestimmt.
Die Kostenfunktion in Abhängigkeit von der Produktionsmenge sei
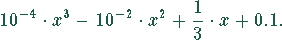
Die Wirtschaftlichkeit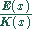 
ist dann ein Quotient aus zwei
Polynomen
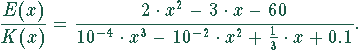
Die Abbildung
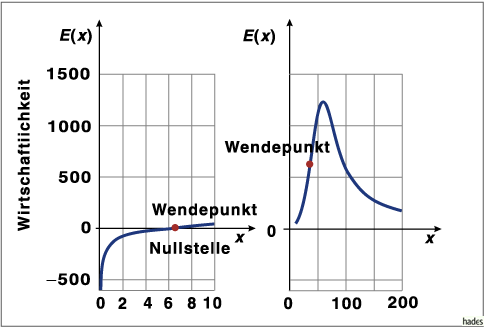
zeigt den Verlauf der Wirtschaftlichkeit mit der Produktionsmenge.
Definitionsbereich:
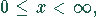
da negative Werte der Produktionsmenge x ökonomisch sinnlos sind.
Nullstellen:
Die Nullstellen sind die Nullstellen des Zählerpolynoms
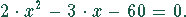
Der Zähler ist ein Polynom zweiten Grades, die Nullstellengleichung deshalb eine quadratische Gleichung. Die Lösungen sind
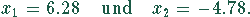
Die zweite Lösung ist negativ und liegt deshalb außerhalb des Definitionsbereiches. Innerhalb des Definitionsbereiches gibt es also nur eine Nullstelle.
Polstellen:
Polstellen liegen an den Nullstellen des Nennerpolynoms. Das Nennerpolynom ist dritten Grades und die Nullstellengleichung also eine kubische Gleichung:
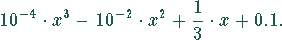
Zur Lösung kann Mathematica oder MapleV verwendet werden.
Mathematica
NSolve[10^(-4) x^3-10^(-2) x^2+(1/3) x+0.1==0,x]
MapleV
solve(10^(-4)*x^3-10^(-2)*x^2+(1/3)*x+0.1=0,x);
Es existieren eine reelle und zwei komplexe Lösungen. Die reelle Lösung
liegt bei 
und damit außerhalb des Definitionsbereiches.
Komplexe Lösungen spielen in der Ökonomie keine Rolle.
Die Funktion der Wirtschaftlichkeit hat innerhalb des Definitonsbereiches
keine Polstellen.
Extremwert
Die erste Ableitung der Wirtschaftlichkeit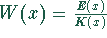 
kann nach der Quotientenregel berechnet werden und lautet:
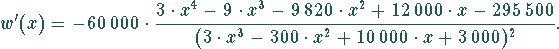
Die erste Ableitung wird null an den Nullstellen des Zählerpolynoms:
Die Nullstellen können mittels der Regula falsi, dem Newton-Verfahren oder nach Bairstow ermittelt werden.
Man erhält nur zwei reelle Nullstellen. Davon ist eine negativ und die andere positiv. Nur die positiven Nullstellen haben in dem Beispiel Bedeutung. Sie lauten:
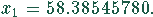
Die zweite Ableitung liefert eine Information über die Art der Extrema (Maximum oder Minimum).
Die zweite Ableitung lautet:
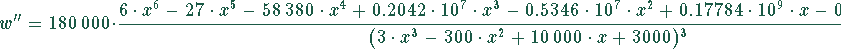
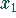in diese zweite Ableitung eingesetzt liefert
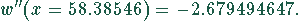
Die zweite Ableitung ist für diesen Wert negativ, d.h., fü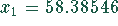r 
liegt ein
Maximum vor.
Zur Untersuchung der Extremwerte dieser Funktion können mit Vorteil die Programme Mathematika oder MapleV verwendet werden. Dazu sind folgende Programmzeilen in diesen Programmen einzufügen und mit < Enter> abzuschließen.
Mathematica
w:=(2 x^2-3 x-60)/(10^(-4) x^3-10^(-2) x^2+(1/3) x+0.1)
Plot[w,{x,0,200}]
w1=D[w,x]
ww1=Simplify[w1]
NSolve[ww1==0,x]
w2=D[ww1,x]
ww2=Simplify[w2]
x=58.38546
ww2
MapleV
w:=(2*x^2-3*x-60)/(10^(-4)*x^3-10^(-2)*x^2+(1/3)*x+0.1) plot(w,x=0..200); w1:=diff(w,x); ww1:=simplify(w1); solve(ww1=0,x); w2:=diff(ww1,x); x:=58.38546; w2;
