|
|
|
|
|
|
|
|
Ein Ofen liefert in der ersten Stunde nach einer Reparatur
des Ofenraumes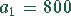 
kg Aluminiumschmelze. Jede weitere Stunde
nimmt der Ausstoß um 
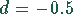kg ab. Die Selbstkosten je Stunde betragen
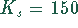DM. Die zur Erreichung der maximal möglichen Schmelzmenge erforderliche
Instandsetzung des Ofenraumes kostet 
DM. Nach welcher Zeit muß der
Ofenraum repariert werden, damit die Kosten pro kg Schmelze ein Minimum
werden?
Die Kostenfunktion ist nur für positive Zeiten t definiert.
Lösung:
Gesucht ist die Zeit t. Die anfallenden Kosten in dieser Zeit sind
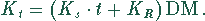
In der ersten Stunde werden 
kg Schmelze erzeugt.
In der zweiten Stunde werden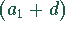 
kg Schmelze erzeugt.
In der dritten Stunde werden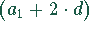 
kg Schmelze erzeugt.
In der t-Stunde werden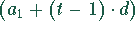 
kg Schmelze erzeugt.
Das in t Stunden erzeugte Schmelzgut beträgt
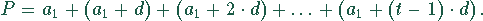
Dies ist eine arithmetische Reihe. Die Summenformel lautet:
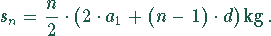
Damit ergibt sich für das gesamte Schmelzgut nach 
Stunden
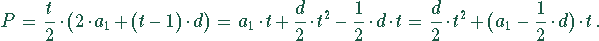
Die Kosten pro kg Schmelze betragen
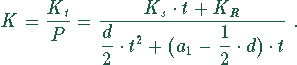
Das Minimum wird durch Nullsetzen der ersten Ableitung von K ermittelt. Die erste Ableitung kann man mittels der Quotientenregel herleiten:
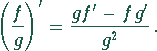
In unserem Fall ist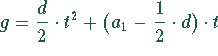 
und
.
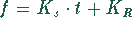Damit erhält man
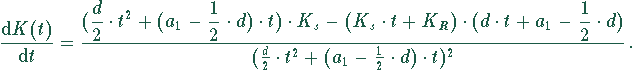
Diese Ableitung wird null, wenn der Zähler null wird:
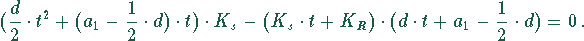
Das liefert die quadratische Gleichung
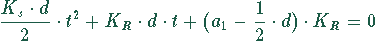
bzw.
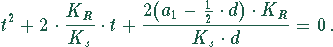
Mit den Zahlenwerten ergibt sich
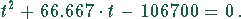
Die Lösungen sind
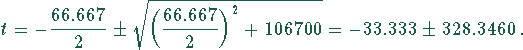
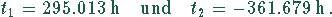
Die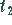 
ist ökonomisch Unsinn.
Die Reparatur muß nach 294 Stunden erfolgen.
Die Abbildung zeigt die Kostenfunktion.
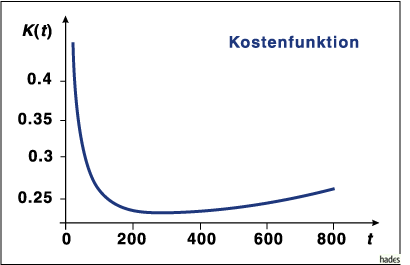
Eine allgemeine Lösung kann man wieder leicht mit Mathematica oder MapleV finden.
Mathematica
y=D[(Ks t+KR)/(d/2. t^2 +(a1-d/2) t),x] Solve[y==0,x]
MapleV
y=diff((Ks*t+KR)/(d/2.*t^2 +(a1-d/2)*t),x); solve(y=0,x);
