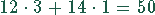|
|
|
|
|
|
|
|
Für die Aufzucht von Vieh ist eine Mischung von zwei Futtersorten vorgesehen.
Eine Mengeneinheit der Futtersorte A enthält 9 Einheiten Kohlehydrate, 6 Einheiten Eiweiße und verursacht 12 DM an Selbskosten.
Die Futtersorte B enthält pro Mengeneinheit 6 Einheiten Kohlenhydrate, 3 Einheiten Eiweiße und 8 Einheiten Fette. Die Selbstkosten betragen 14 DM.
Aus biologischen Gründen sollen in der Futtermischung mindestens 18 Einheiten Kohlenhydrate, 24 Einheiten Eiweiße und 8 Einheiten Fette vorhanden sein.
Wie müssen die Futtersorten gemischt werden, um die Kosten zu minimieren?
Lösung:
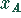-- Anzahl der Mengeneinheiten der Futtersorte A
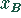-- Anzahl der Mengeneinheiten der Futtersorte B
Die Zielfunktion hat die Gleichung
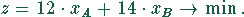
Als einschränkende Bedingungen gelten
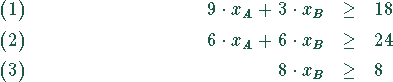
Die Nichtnegativitätsbedingung lautet:
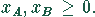
Die Nichtnegativitätsbedingung schränkt die Lösungsmenge auf den ersten Quadranten der reellen Zahlenebene ein. Die Nebenbedingungen bilden weitere Grenzen für die Lösungsmengen. Aus (1) folgt die Geradengleichung
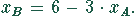
Aus (2) folgt
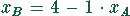
und aus (3)
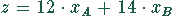
stellt eine Geradengleichung dar.
Da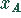 
und 
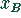natürliche Zahlen sein müssen,
muß z sowohl durch 12 als auch durch 14
teilbar sein, damit die Schnittpunkte dieser Geraden zu den natürlichen
Zahlen gehören. Dies wird für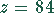 
erfüllt.
Diese Gerade muß nun nach links parallel verschoben werden,
bis sie das Gebiet der Lösungsmenge nur in einem Punkt berührt.
Dies ergibt die Abbildung.
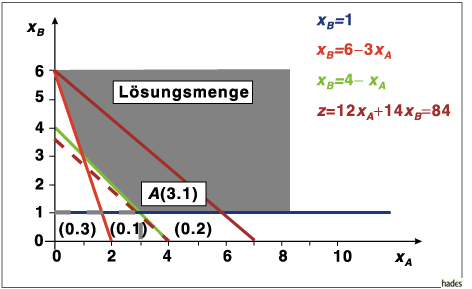
Im Punkt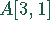 
ist das gesuchte Minimum. Die Zielfunktion nimmt den
Wert
an.
