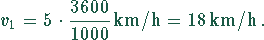|
|
|
|
|
|
|
|
Die Anzahl z der Fahrzeuge, die stündlich eine Straße passieren können, läßt sich aus der mittleren Geschwindigkeit v (m/s) und der mittleren Länge l (m) dieser Fahrzeuge berechnen. Die empirisch gefundene Formel für diese Berechnung lautet:
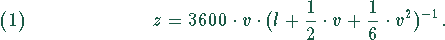
Bei welcher Geschwindigkeit v, gemessen in (km/h), wird der Durchlaß am größten?
Gegeben: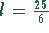 
m.
Lösung:
Die Extremwerte einer Funktion findet man durch Nullsetzen der ersten Ableitung. Das Vorzeichen der zweiten Ableitung an dieser Stelle gibt eine Information über die Art des Extremums (Maximum oder Minimum). Die erste Ableitung von (1) liefert
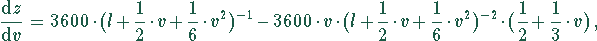
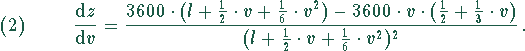
Diese erste Ableitung wird Null, wenn der Zähler Null wird. Das ergibt die Gleichung
Aus (5) folgt
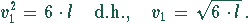
Um zu prüfen, was für ein Extremum vorliegt, muß die zweite Ableitung an dieser Stelle gebildet werden. Die Gleichung (2) wird etwas vereinfacht
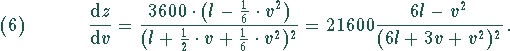
Daraus errechnet man die zweite Ableitung nach den Regeln der Differentation zu
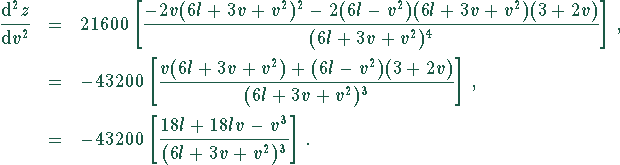
Setzt man 
, so ergibt sich
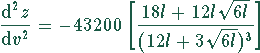
Die zweite Ableitung ist an der Stelle 
negativ.
In diesem Fall ist das gefundene
Extremum ein Maximum.
Mit den Zahlenwerten ergibt sich:
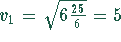m/s.
Für die Geschwindigkeitsangabe km/h muß dieser Wert mit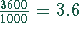 
multipliziert werden:
Bei dieser Geschwindigkeit ist der Durchlaß
am größten.
