|
|
|
|
|
|
|
|
Mittels einer Wheatstoneschen Brücke und eines Vergleichswiderstandes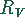 
sowie
eines Schiebewiderstandes der Länge l wird der Wert eines Widerstandes R
gemäß
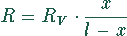
gemessen. Dabei ist x die Länge auf dem Schiebewiderstand, bei dem der
Querstrom in der Brücke verschwindet. Der Ablesefehler 
von x
ist konstant. Für welches x ist der relative Fehler der Widerstandsmessung
am kleinsten? Wie groß ist er?
Lösung:
Den relativen Fehler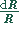 
erhält man durch Differentiation
des Logarithmus der Widerstandsfunktion:
Die Differentiation liefert
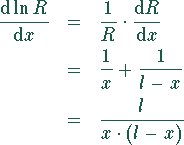
Wird diese Beziehung mit 
multipliziert, so ergibt sich
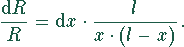
Der relative Fehler soll ein Minimum, das heißt ein Extremwert
der Funktion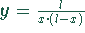 
sein. Extremwerte findet man durch
Nullsetzen der ersten Ableitung. Die erste Ableitung dieser Funktion lautet:
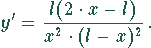
Diese Ableitung wird an der Stelle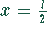 
null. An dieser
Stelle nimmt also der relative Fehler der Widerstandsmessung einen
Extremwert an.
Ob dieser Extremwert ein Minimum ist, kann aus der zweiten Ableitung ersehen werden.
Die zweite Ableitung ergibt:
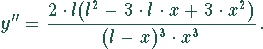
Einsetzen von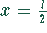 
liefert
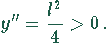
Deshalb liegt an der Stelle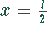 
ein Minimum des relativen Fehlers
vor.
Der minimale relative Fehler hat den Wert
