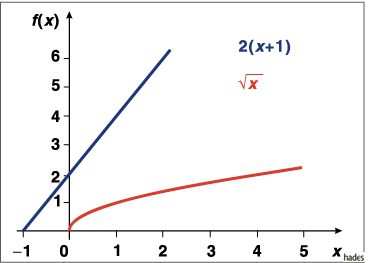
|
|
|
|
|
|
|
|
Welche kürzeste Entfernung besteht zwischen der Geraden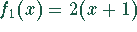 
und der
Parabel 
?
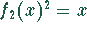Lösung:
Der Abstand kann nach folgender Beziehung errechnet werden:
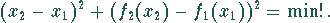
Gleichzeitig gilt
Das ergibt folgende Beziehung
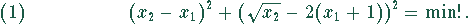
Das ist eine Bestimmungsgleichung mit zwei Unbekannten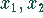 
für den Extremwert, deshalb müssen die partiellen Ableitungen nach diesen
Unbekannten null sein.
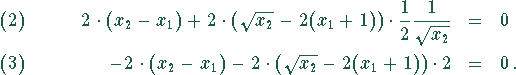
Ein Umrechnung ergibt die zwei Gleichungen für zwei Unbekannte
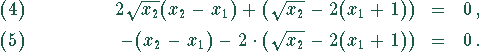
Durch Multiplikation von (4) mit 2 und Addition beider Gleichungen erhält man
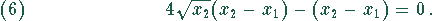
Daraus ergibt sich
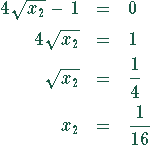
Setzt man diesen Wert in (5) ein, so erhält man eine Gleichung für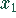 
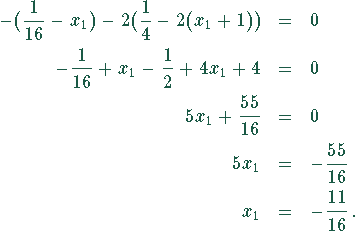
Durch Einsetzen dieser Werte in die Funktionsgleichungen erhält man die
Punkte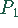 
und 
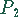auf der Geraden bzw. Parabel, die den kleinsten Abstand
voneinander haben.
